Dans un cercle, deux cordes de même longueur sont à égale distance du centre de ce cercle.
Explications :
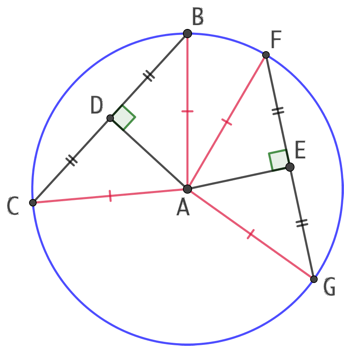
Soit un cercle de centre A. [BC] et [FG] sont deux cordes de ce cercle. On suppose que 
.
Soit D et E les projetés orthogonaux de A sur les cordes [BC] et [FG]. AD est la distance entre A et la corde [BC], et AE la distance entre A et la corde [FG].
D’après la proposition III.3 d’Euclide, D est le milieu de [BC]. On démontre de la même façon que E est le milieu de [FG].
Comme , on a 
. Par ailleurs on a 
. Puisque les triangles ABD et AEF sont rectangle, d’après le théorème de Pythagore, il vient que 
. Donc les deux cordes sont à égale distance de A.
Remarque : Il s’agit de la proposition III.14 des Éléments d’Euclide.
