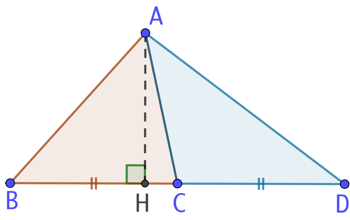
C est le milieu de [BD]. Alors les deux triangles ABC et ACD ont la même aire.
Explications :
ABC et ACD ont un sommet en commun : A. Par conséquent la (AH) est la hauteur issue de A commune aux deux triangles.
Leur base, côté opposé au sommet A, [BC] et [CD] ont la même longueur.
On nous savons que l’aire d’un triangle est égale à la hauteur multipliée à la base et divisée par deux.
L’aire de ABC est 
. L’aire de ACD est 
. Puisque 
, il vient que les deux aires sont égales.
Remarque : On démontre très simplement que si deux triangles de même aire; ABC et ACD, tels que B, C et D soient alignés, alors C est le milieu de [BD].
