Deux triangles isométriques se superposent.
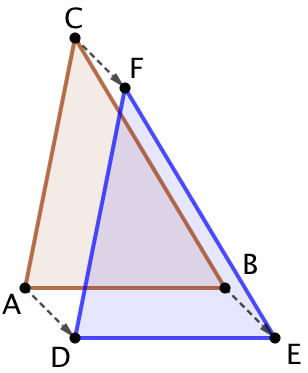
Soient deux triangles ABC et DEF possédant des côtés de longueur égale deux à deux. On peut alors observer que les triangles se superposent, A sur D, B sur E et C sur F.
Explications :
Supposons que ces deux triangles ne se superposent pas parfaitement et que par exemple, ayant placé D sur A et E sur B, F ne soit pas placé sur C.
On se retrouve alors exactement dans la situation décrite par l’article : une figure impossible et qui conclut sur le fait que nécessairement C et F doivent être confondus.
Remarque : Il s’agit de la proposition I.8 des Éléments d’Euclide.
