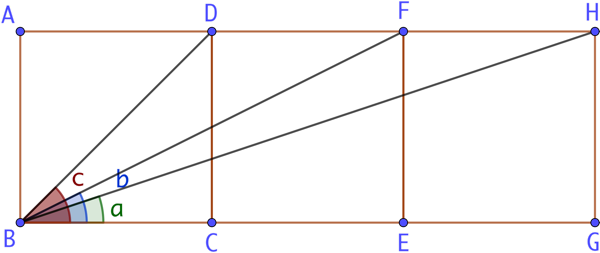
Etant données trois carrés identiques, la sommes des mesures des angles GBH et GBF est égale à la mesure de l’angle GBD, soit d’après la figure : a + b = c = 45°.
Réponse par une construction géométrique :
Nous savons que l’angle GBD a la même mesure que l’angle CBD qui vaut 45° puisque c’est l’angle que fait un côté d’un carré avec l’une de ces diagonales.
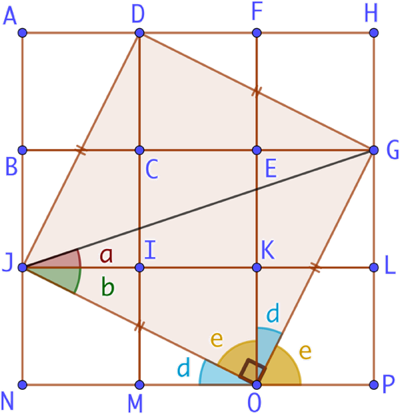
On complète la figure en ajoutant six carrés identiques aux trois premiers.
L’angle LJG mesure a et l’angle LJO mesure b.
Nous construisons un quadrilatère DJOG. Ses quatre côtés ont la même longueur puisqu’ils sont les diagonales de quatre rectangles identiques. DJOG est donc un losange.
Par ailleurs, l’un des angles de DJOG, l’angle GOJ, mesure d + e. Or l’angle KOM mesure également d + e. Mais KOMI étant un carré, l’angle KOM mesure 90°. Par conséquent d + e = 90°. On peut donc affirmer que l’angle GOJ mesure également 90°. Mais nous savons qu’un losange dont l’un des angles mesure 90° est nécessairement un carré. Nous en concluons que DJOG est un carré.
Donc le segment [JG] est la diagonale d’un carré et il fait avec le côté [JO] un angle OJG de 45°. Or OJG = a + b. Conclusion a + b = 45° = c.
Réponse trigonométrique à partir la première figure :
Règle de calcul : tan(a + b) = (tan(a) + tan(b)) / (1 – tan(a)tan(b))
Supposons que chaque côté des carrés mesure t.
- tan(a) = HG / BG = t / 3t = 1/3
- tan(b) = FE / BE = t / 2t = 1/2
- tan(a + b) = (1/3 + 1/2) / ( 1- 1/3 x 1/2) = 1
- tan(c) = t/t = 1
- Donc tan(c) = tan(a + b)
Etant donné que tous ces angles ont des mesures comprises entre 0 et 90°, on peut en conclure que c = a + b.
