3 carrés sur un cercle

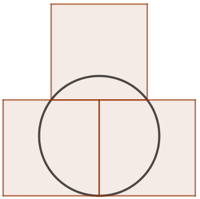
Trois carrés identiques de côté 1 unité de longueur recouvrent un cercle comme indiqué sur la figure. On cherche à déterminer le rayon du cercle.

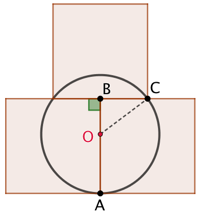Explications (première méthode) :

Théorème de Pythagore sur OCB : OC^2 = OB^2 + BC^2. (1)

Sachant que OB = AB - AO = 1 - OC, L’équation (1) devient : OC^2 = (1 - OC)^2 + \dfrac{1}{4}.

Après simplification, il vient : OC = \dfrac{5}{8}.

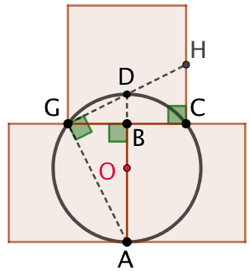Explications (deuxième méthode) :

On va calculer le rayon OD. Les triangles ABG et HCG sont isométriques :

  • un côté de même longueur : CG = AB = 1 ;
  • (CG) et (AB) sont perpendiculaires ;
  • (AG) et (HG) sont perpendiculaires.

Donc HC = BG = \dfrac{1}{2}.

Par construction les droites (BD) et (CH) sont parallèles. B est le milieu du segment [GC]. Donc d’après le théorème des milieux, BD = \dfrac{HC}{2} = \dfrac{1}{4}.

Finalement AD = AB + BD = 1 + \dfrac{1}{4} = \dfrac{5}{4}. Ce qui donne OD = \dfrac{5}{8}.

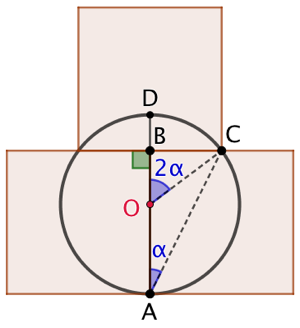Explications (troisième méthode, pourquoi faire simple quand on peut faire compliqué) :

On va calculer le rayon OC du cercle.

\tan(\alpha)=\dfrac{BC}{BA} = \dfrac{1}{2} et \tan(2 \alpha)=\dfrac{BC}{BO} = \dfrac{1}{2 \times BO}

Propriété trigonométrique : \tan(2 \alpha) = \dfrac{2 \tan(\alpha)}{1 - \tan^2 \alpha} = \dfrac{4}{3}

Donc \dfrac{1}{2 \times BO} = \dfrac{4}{3}, ce qui donne OB = \dfrac{3}{8}.

Théorème de Pythagore sur OCB : OC^2 = OB^2 + BC^2 = \dfrac{9}{64} + \dfrac{1}{4} = \dfrac{25}{64}. Donc OC = \dfrac{5}{8}.

 

Print Friendly, PDF & Email