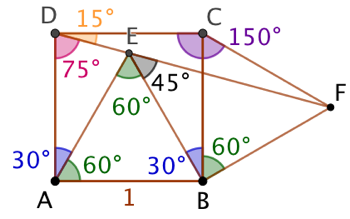
 Étant donné un carré ABCD et deux triangles équilatéraux ABE et BCF de longueur de côté égale à celle du carré, on montre que les trois points D, E et F sont alignés.
Étant donné un carré ABCD et deux triangles équilatéraux ABE et BCF de longueur de côté égale à celle du carré, on montre que les trois points D, E et F sont alignés.
Pour les deux explications qui suivent, il est intéressant de commencer par déterminer les mesures de tous les angles de la figure, à l’aide des propriétés des carrés, des triangles rectangles, des triangles isocèles ou équilatéraux.
Première explication : on va démontrer que ![]() .
.
Pour simplifier les calculs, on prend la longueur du côté du carré comme unité de mesure.
Formule d’Al-Kashi dans le triangle ADE : ![]()
![]() . Donc
. Donc ![]()
Formule d’Al-Kashi dans le triangle CDF : ![]()
![]() . Donc
. Donc ![]()
Théorème de Pythagore dans le triangle EBF rectangle en B : ![]() . Donc
. Donc ![]()
Il reste à vérifier par le calcul que ![]() . On y arrive en élevant deux fois au carré les membres de l’expression.
. On y arrive en élevant deux fois au carré les membres de l’expression.
Seconde explication : on va démontrer que l’angle ![]() est plat.
est plat.
![]() .
.
