Soit un carré ABCD. On construit dans ce carré les triangles équilatéraux ABE et BCE. On veut démontrer que le petit triangle FED est aussi équilatéral.
On démontre dans un premier temps que FED est isocèle en D :
ABE est équilatéral donc l’angle ABE mesure 60°. D est situé sur la diagonal du carré ABCD donc l’angle ABD mesure 45°. Par conséquent l’angle DBE mesure 60°- 45° = 15°. On démontrerait de la même façon que DBF mesure aussi 15°. Donc (BD) est la bissectrice de l’angle EBF et, on note pour le second temps de cette démonstration que l’angle EBF mesure 2 x 15 = 30°.
Or le triangle EBF est isocèle en B car les deux triangles équilatéraux ont les mêmes dimensions. par conséquent (BD) est aussi la médiatrice de [EF] et elle coupe [EF] en son milieu H. D étant sur la médiatrice de [EF], D est équidistant de E et de F. Ce qui démontre que le triangle DEF est isocèle en D.
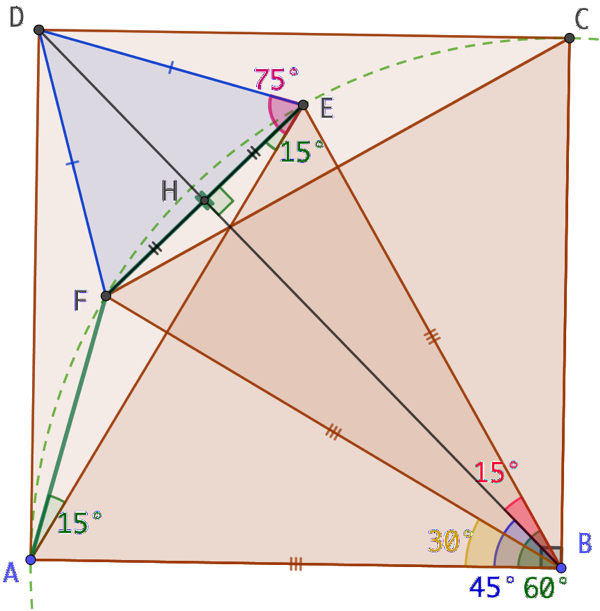
On démontre dans un second temps que, par exemple, que l’angle DEF mesure 60° :
Puis que l’angle ABC est droit et que l’angle FBC mesure 60°, il vient que l’angle ABF mesure 30°. Mais l’angle FBE mesure aussi 30°. De plus les triangles ABF et FBE ont deux côtés de même longueur, ils sont isométriques. On en conclut que les côtés AF et FE ont la même longueur. Par conséquent FAE est isocèle en F.
L’angle EAF est un angle inscrit qui intercepte le même arche cercle EF que l’angle au centre EBF qui mesure 30°; donc EAF mesure 15°. Comme FAE est isocèle en F, on en déduit que l’angle FEA mesure aussi 15°.
Or le triangle EAD est par construction isocèle en A. Si son angle au sommet mesure 30°, ces deux angles à la base mesure chacun 75°, en particulier l’angle DEA. Mais l’angle DEA est la somme des angles DEF et FEA. Sachant que FEA mesure 15°, on en conclut que DEF mesure 75 – 15 = 60°.
Conclusion DEF est un triangle isocèle dont l’un des angles mesure 60°, il est donc équilatéral.
