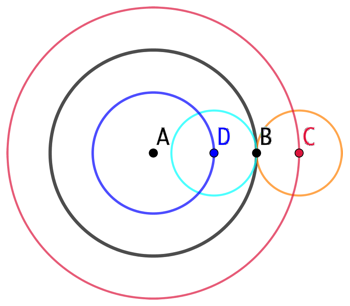Soient un cercle de centre A et de rayon AB (cercle noir) et 
une longueur fixe. Le lieu géométrique des centres des cercles extérieurs tangents au premier cercle et de rayon , est un cercle de centre A et de rayon 
(cercle rouge). Le lieu géométrique des centres des cercles intérieurs au premier cercle et tangents à celui-ci est un cercle de centre A et de rayon 
(cercle bleu).
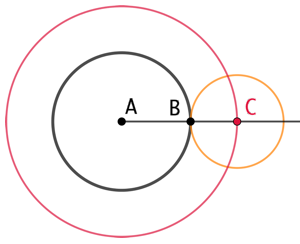Si les cercles de centre A et C, passant par B sont tangents en B, alors les points A, B et C sont alignés. 
. Comme 
et sont des rayons de valeur fixe, la distance AC reste constante quand B décrit le cercle de centre A. Par conséquent le point C décrit un cercle de centre A et de rayon 
.
On ferait la même démonstration pour les centres des cercles intérieurs tangents au cercle de centre A.
