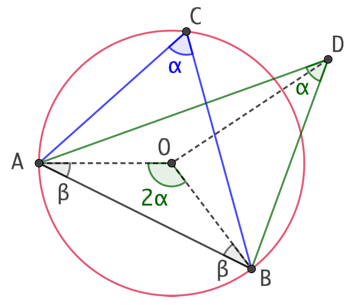
Soient le cercle circonscrit au triangle ABC et un point D situé du même côté que C par rapport à la droite (AB). Ces quatre points seront cocycliques si 
.
Explications :
Raisonnons par l’absurde en supposons que le point D est en dehors du cercle et que .
Considérons le triangle OBD. 
donc 
.
Considérons le triangle ODA. 
donc 
.
Comme 
, il vient 
. (1)
Considérons le triangle ABD. 
. (2)
Or 
et 
.
De (2) il vient 
.
En utilisant (1), on obtient 
. Or, en considérant le triangle OAB, 
et 
.
On aboutit à une conclusion impossible donc D appartient au cercle passant par A, B et C.
On peut aussi supposer que D est à l’intérieur du cercle et développer le même genre de raisonnement par l’absurde.
Corollaire : Soient le cercle circonscrit au triangle ABC et un point D situé du côté opposé à C par rapport à la droite (AB). Ces quatre points seront cocycliques si 
et 
sont supplémentaires.
