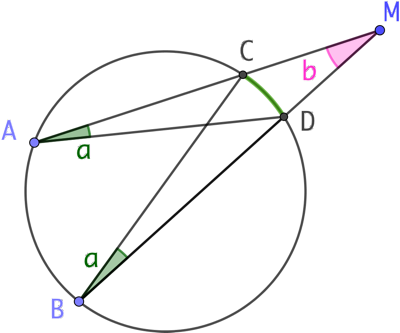
 Etant donnés un cercle et un point M, on choisit deux points quelconques A et B sur le cercle. On trace les segments [MA] et [MB] qui coupent le cercle aux points C et D.
Etant donnés un cercle et un point M, on choisit deux points quelconques A et B sur le cercle. On trace les segments [MA] et [MB] qui coupent le cercle aux points C et D.
On démontre l’égalité suivante entre les distances : ![]() .
.
Explications :
Les angles CAD et CBD interceptant le même arc de cercle CD, ils ont donc la même mesure.
 Puisque les triangles MAD et MCB ont deux angles de même mesure, ils sont semblables.
Puisque les triangles MAD et MCB ont deux angles de même mesure, ils sont semblables.
On a alors l’égalité : ![]() que l’on peut écrire ainsi :
que l’on peut écrire ainsi : ![]() .
.
Le produit ![]() ne dépend que de la position du point M par rapport au cercle mais il est indépendant du choix du segment issu de M et rencontrant le cercle. Ce produit est la puissance du point par rapport au cercle.
ne dépend que de la position du point M par rapport au cercle mais il est indépendant du choix du segment issu de M et rencontrant le cercle. Ce produit est la puissance du point par rapport au cercle.
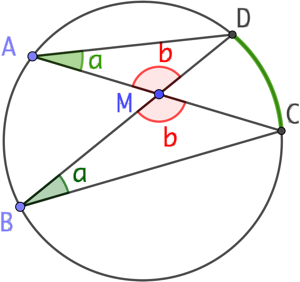
Remarque : On obtient exactement le même résultat si le point M se situe à l’intérieur du cercle.
Voir aussi : Puissance d’un point et tangente à un cercle
Remarque : Il s’agit de la proposition III.35 des Éléments d’Euclide.
