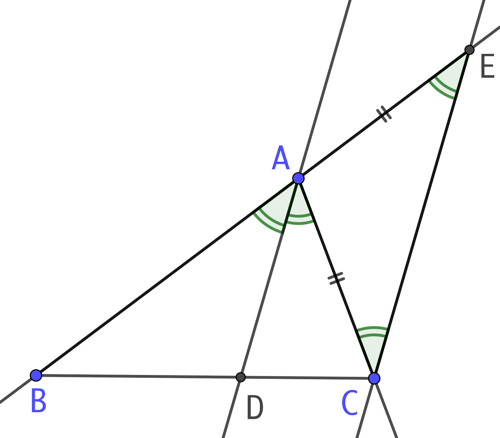
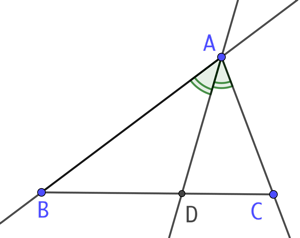
 La bissectrice de l’angle BAC coupe le côté BC au point D. On démontre l’égalité des rapports des longueurs :
La bissectrice de l’angle BAC coupe le côté BC au point D. On démontre l’égalité des rapports des longueurs : ![]()
Explications :
On complète la figure par une droite (CE) parallèle à (AD) et qui coupe la droite (AB) au point E.
On peut alors écrire les égalités de mesures d’angles suivantes :
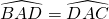 car la droite (AD) est la bissectrice de BAC.
car la droite (AD) est la bissectrice de BAC.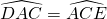 car les droites (AD) et (EC) sont parallèles donc les deux angles alternes-internes ont la même mesure.
car les droites (AD) et (EC) sont parallèles donc les deux angles alternes-internes ont la même mesure.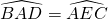 car les droites (AD) et (EC) sont parallèles donc les deux angles correspondants ont la même mesure.
car les droites (AD) et (EC) sont parallèles donc les deux angles correspondants ont la même mesure.- Donc
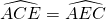 . Ce qui permet de conclure que le triangle AEC est isocèle en A et que les longueurs AE et AC sont égales.
. Ce qui permet de conclure que le triangle AEC est isocèle en A et que les longueurs AE et AC sont égales.
On applique le théorème de Thales sur le triangle BEC : ![]() . Comme
. Comme ![]() , l’égalité des rapports devient :
, l’égalité des rapports devient : ![]() .
.