Rectangle et carré de même aire

Étant donnée une longueur a, on veut construire un rectangle et un carré de même aire. On impose que a soit la plus grande longueur du rectangle.

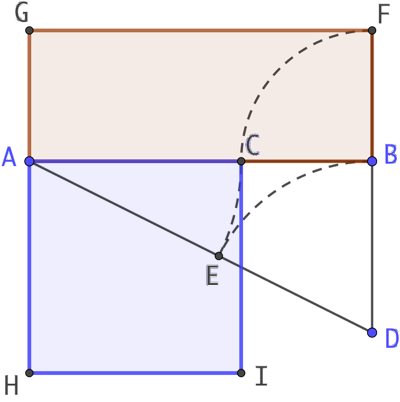
Construction :

  • On trace un segment [AB] de longueur a.
  • On trace la perpendiculaire à (AB) passant par B.
  • On place le point D tel que BD = AB / 2.
  • On trace le segment [AD].
  • On place le point E intersection de (AD) et du cercle de centre D et de rayon BD.
  • On place le point C intersection de (AB) et du cercle de centre A et de rayon AE.
  • On place le point F intersection de (BD) et du cercle de centre B et de rayon BC,  puis on complète le rectangle ABFG.
  • On trace le carré de côté AC. Ce carré et le rectangle possède la même aire.

Explications :

Le théorème de pythagore dans le triangle ABD donne : AD^2 = AB^2 + BD^2 = a^2 + \dfrac{a^2}{4} = \dfrac{5a^2}{4}. Donc AC = AE = AD - ED = \dfrac{a\sqrt{5}}{2} - \dfrac{a}{2} = \dfrac{a}{2}(\sqrt{5}-1)}.

L’aire du carré est : (\dfrac{a}{2}(\sqrt{5}-1)})^2 = \dfrac{a^2}{4}(5 - 2\sqrt{5} + 1) = \dfrac{a^2}{2}(3 - \sqrt{5})

La hauteur du rectangle est FB = CB = AB - AC = a - \dfrac{a}{2}(\sqrt{5}-1)} = \dfrac{a}{2}(3 - \sqrt{5})}
L’aire du rectangle est = a \times \dfrac{a}{2}(3 - \sqrt{5})}. On retrouve bien l’aire du carré.

Est-ce la seule solution ?

Supposons qu’une telle solution existe, à savoir un rectangle de longueur a et de hauteur h < a et un carré de côté c avec c = a - h, tels que leur aire soit égale. L’aire du rectangle est ah et l’aire du carré est \dfrac{a-h}{2}. L’équation à résoudre est alors : ah = \dfrac{a-h}{2}, soit h^2 - 3ah + a^2 = 0. Le discriminant est 5a^2 > 0. L’équation possède deux solutions : \dfrac{a}{2}(3 + \sqrt{5}) et \dfrac{a}{2}(3 - \sqrt{5}). La première solution ne peut pas être retenue car h < a. Il reste donc \dfrac{a}{2}(3 - \sqrt{5}). Le côté du carré est c = a - \dfrac{a}{2}(3 - \sqrt{5}) = \dfrac{a}{2}(\sqrt{5}-1)}. On retrouve la solution et elle est unique.

Print Friendly, PDF & Email