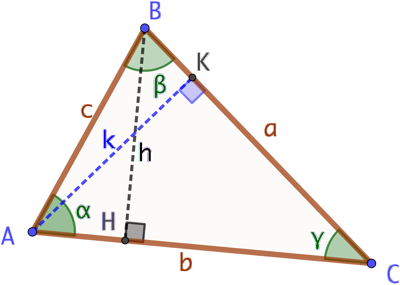
Étant donné un triangle ABC quelconque, la loi des sinus s’exprimer ainsi : ![]()
Explications :
![]() donc
donc ![]()
De même : ![]() donc
donc ![]()
si ![]() alors
alors ![]()
![]() donc
donc ![]()
De même : ![]() donc
donc ![]()
si ![]() alors
alors ![]()
Conclusion : ![]()
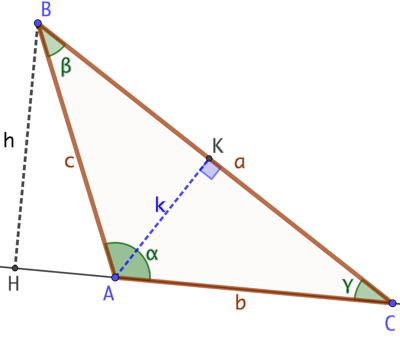 Remarque si un des angles est obtus :
Remarque si un des angles est obtus :
![]() …
…
Ce qui est affirmé sans preuve peut être nié sans preuve (Euclide). Le but ultime n'est rien, le mouvement est tout (Eduard Bernstein)


Étant donné un triangle ABC quelconque, la loi des sinus s’exprimer ainsi : ![]()
Explications :
![]() donc
donc ![]()
De même : ![]() donc
donc ![]()
si ![]() alors
alors ![]()
![]() donc
donc ![]()
De même : ![]() donc
donc ![]()
si ![]() alors
alors ![]()
Conclusion : ![]()
 Remarque si un des angles est obtus :
Remarque si un des angles est obtus :
![]() …
…