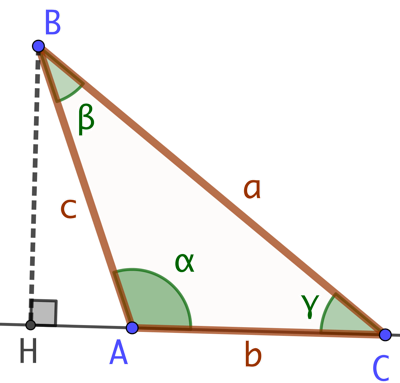
 Étant donné un triangle ABC quelconque, la loi des cosinus s’exprime ainsi :
Étant donné un triangle ABC quelconque, la loi des cosinus s’exprime ainsi : ![]() . Il s’agit de la généralisation du théorème de Pythagore à un triangle non rectangle.
. Il s’agit de la généralisation du théorème de Pythagore à un triangle non rectangle.
Explications :
Pythagore dans le triangle AHB donne : ![]() .
.
Or ![]() et
et ![]() .
.
Donc ![]()
Soit ![]()
On met ![]() en facteur et on rappelle que
en facteur et on rappelle que ![]() .
.
Ce qui donne ![]() .
.
Conclusion : ![]()
Remarque si un des angles du triangle est obtus :
![]() …
…