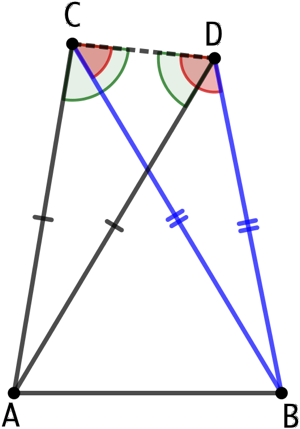
 Il est impossible de construire la figure suivante dans laquelle AC = AD et BC = BD avec les points C et D distincts et situés du même côté de la droite (AB).
Il est impossible de construire la figure suivante dans laquelle AC = AD et BC = BD avec les points C et D distincts et situés du même côté de la droite (AB).
Explications :
Supposons cette figure existante. Alors les triangles CAD et CBD sont isocèles. Cela conduit aux égalités de mesures d’angles suivantes : ![]() et
et ![]() .
.
Or : ![]()
Donc ![]()
Soit ![]()
Ce qui donne ![]()
Ce qui est impossible car ![]() ne peut pas être strictement supérieur à lui-même.
ne peut pas être strictement supérieur à lui-même.
Remarque : Il s’agit de la proposition I.7 des Éléments d’Euclide.
