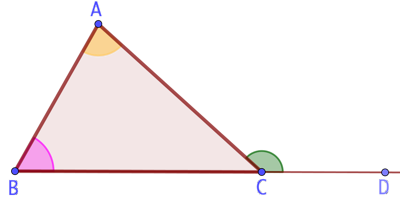
 Étant donné un triangle ABC et un point D sur la droite (BC), les deux angles du triangle opposés au sommet C, à savoir
Étant donné un triangle ABC et un point D sur la droite (BC), les deux angles du triangle opposés au sommet C, à savoir ![]() et
et ![]() ont une mesure inférieure à celle de l’angle
ont une mesure inférieure à celle de l’angle ![]() .
.
Explications :
J’utilise le raisonnement employé par Euclide sans faire une référence explicite aux propriétés d’un parallélogramme.
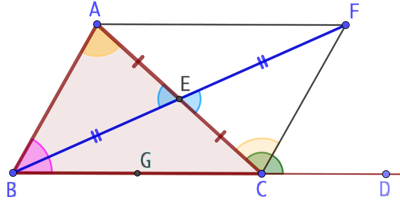
On place E milieu de [AC] et F symétrique de B par rapport à F. ![]() car ce sont des angles opposés par le sommet.
car ce sont des angles opposés par le sommet.
 Par construction nous avons les égalités de distances : AE = EC et BE = EF. Par conséquent les triangles AEB et CEF sont isométriques. Ce qui permet d’affirmer que
Par construction nous avons les égalités de distances : AE = EC et BE = EF. Par conséquent les triangles AEB et CEF sont isométriques. Ce qui permet d’affirmer que ![]() , c’est à dire
, c’est à dire ![]() . Comme
. Comme ![]() , on en conclut que
, on en conclut que ![]() .
.
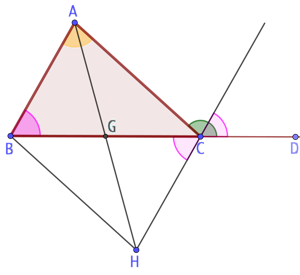
On montrerait de la même manière que ![]() .
.
Remarque : Il s’agit de la proposition n°I.16 des Éléments d’Euclide.