 Étant donnés un cercle de centre O et de rayon r, et un vecteur
Étant donnés un cercle de centre O et de rayon r, et un vecteur ![]() de norme inférieur à 2r, comment placer deux points C et D sur le cercle afin
de norme inférieur à 2r, comment placer deux points C et D sur le cercle afin ![]() ?
?
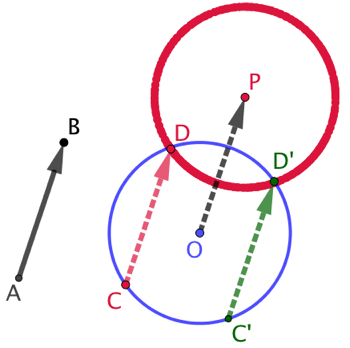
Construction :
- On choisit un point C quelconque sur le cercle et on construit le point D tel que
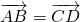 .
. - Quand le point C parcourt le cercle, le point D parcourt un cercle de centre P de même rayon r et tel que
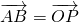 .
. - Les deux points D et D’ intersections des deux cercles permettent de construire les couples (C,D) et (C’,D’) recherchés.
Explications :
On sait que l’image d’un cercle par une translation est un cercle de même rayon et de centre l’image du centre par la translation. (Voir L’image d’un cercle par une translation).
Comme la norme du vecteur ![]() est inférieur au diamètre du cercle, OO’ < 2r, donc le cercle et son image par la translation se croisent en deux points D et D’.
est inférieur au diamètre du cercle, OO’ < 2r, donc le cercle et son image par la translation se croisent en deux points D et D’.
