Étant donné un segment de longueur quelconque, il est toujours possible de le diviser en n parties de même longueur.
Construction : On va partager le segment [AB] en 5 parties de même longueur.
- On trace la perpendiculaire à (AB) passant par A.
- On trace le cercle de centre A passant par B. Celui coupe la perpendiculaire au point C.
- On trace le cercle de centre C passant par A. Il coupe (AC) en D
- On place de la même façon les points E, F et G.
- On trace la droite (BG) puis les droites parallèles à (BG) passant par F, E, D, et C.
- Ces droites coupent (AB) aux points K, J, I et H. Les longueurs AH, HI, IJ, JK et KB sont égales au cinquième de la distance AB.
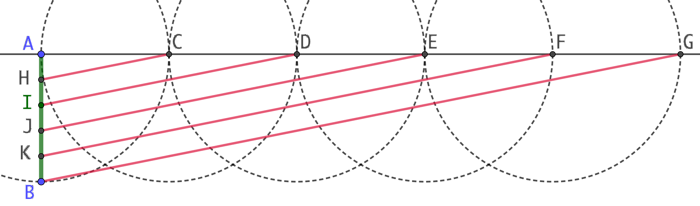
Explication : Théorème de Thalès.
