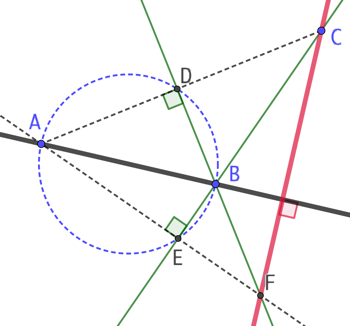
Soit la droite (AB) et un point C n’appartenant pas à cette droite. La droite perpendiculaire à (AB) passant par C se construit ainsi :
- On trace un cercle de diamètre AB passant par A et par B.
- On trace la droite (AC) qui coupe le cercle en D.
- On trace la droite (DB).
- On trace la droite (BC) qui coupe le cercle en E.
- On trace la droite (AE).
- On place le point F intersection des droites (BD) et (AE).
- (CF) est la droite perpendiculaire à (AB) qui était recherchée.
Explications :
AB est un diamètre du cercle et D est sur ce cercle donc le triangle DAB est rectangle en D. Par conséquent les droites (AC) et (BD) sont perpendiculaires
Pour les mêmes raisons, les droites (AE) et (CE) sont perpendiculaires.
Les droites (FD) et (CE) sont deux hauteurs du triangle CAF. Elles se coupent en B qui est donc l’orthocentre du triangle. Donc la droite (AB) est la 3ème hauteur de CAF. Conclusion : (AB) et (CF) sont perpendiculaires.
