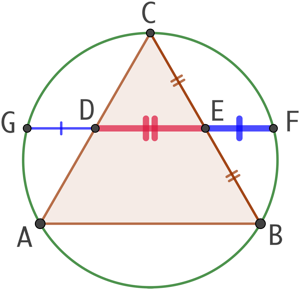
 Étant donné un triangle équilatéral ABC, D et E les milieux respectifs des côtés [AC] et [CB], G et F les points d’intersection de la droite (DE) et du cercle circonscrit à ABC, on démontre que le quotient
Étant donné un triangle équilatéral ABC, D et E les milieux respectifs des côtés [AC] et [CB], G et F les points d’intersection de la droite (DE) et du cercle circonscrit à ABC, on démontre que le quotient ![]() est égal au nombre d’or.
est égal au nombre d’or.
Explications :
On calcule de deux manières différentes la puissance de E par rapport au cercle, ce qui donne l’équation : ![]() (1)
(1)
On observe que :
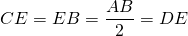 . Car ABC est équilatéral et en vertu du théorème des milieux appliqué au triangle ABC.
. Car ABC est équilatéral et en vertu du théorème des milieux appliqué au triangle ABC.- La construction étant symétrique, on a
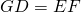 .
.
Par conséquent l’équation (1) devient : ![]() qui se transforme facilement en
qui se transforme facilement en ![]() . On reconnait l’équation
. On reconnait l’équation ![]() dont la solution positive est le nombre d’or
dont la solution positive est le nombre d’or ![]() .
.
