Réciproque du théorème de Pythagore

Soit un triangle ABC tel que AB^2+AC^2=BC^2 alors ce triangle est rectangle en A.

Explications :

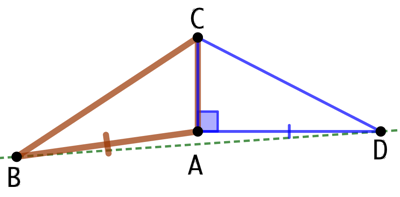
On place un point D tel que CAD soit rectangle en A et AD = AB.

Donc AC^2+AD^2=CD^2. Comme AD = AB, l’égalité devient AC^2+AB^2=CD^2.

Or AB^2+AC^2=BC^2. Donc BC^2 = CD^2 d’où BC=CD.

Puisque CB=CD et AB=AD, la droite (AC) est la médiatrice de [BD], donc (AC) est perpendiculaire à (BD). Mais (AC) est aussi perpendiculaire à (AD). Donc (AD) = (BD) et les points A, B et D sont alignés. Par conséquent ABC est un triangle rectangle en A.

Remarque : Il s’agit de la proposition I.48 des Éléments d’Euclide.

Print Friendly, PDF & Email