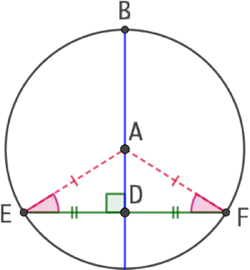
Si une droite passant par le centre d’un cercle coupe une corde de ce cercle par son milieu, elle sera perpendiculaire à cette corde.
Explications :
Il suffit de montrer que (AB) et (EF) sont deux droites perpendiculaires entre elles.
E et F sont deux points du cercle de centre A donc 
, et par conséquent A est sur la médiatrice de [EF].
Par hypothèse (AB) coupe [EF] en son milieu D qui est évidemment sur la médiatrice de [EF].
Donc (AD), c’est-a-dire (BA) est la médiatrice de [EF]. Ce qui permet de conclure par (AB) perpendiculaire à (EF).
RÉCIPROQUE
On peut aussi démontrer que si (AB) est perpendiculaire à (EF) alors (AB) passe par le milieu de [EF].
Explications :
On a toujours comme hypothèse 
donc A est sur la médiatrice de [EF]. Or (AB) est perpendiculaire à (EF) donc (AB) est la médiatrice de [EF]. Par hypothèse D est sur la droite (AB) donc 
. Comme E, D et F sont alignés, on peut conclure que D est le milieu de [EF] et que (AB) passe par le milieu de [EF].
Conséquence : Le centre du cercle appartient aux médiatrices de toutes les cordes de ce cercle.
Remarque : Il s’agit de la proposition III.3 des Éléments d’Euclide.
Euclide n’utile pas la notion de médiatrice d’un segment. Il démontre que les triangles AED et ADF sont semblables, donc que 
.
