Cordes et diamètres d’un cercle

Étant donné un point F appartenant à un diamètre [BC] d’un cercle et différent du centre A de ce cercle,

1. tout segment délimité par F et un point E quelconque du cercle aura une longueur supérieure à FC et inférieure à FB.
2. La longueur FE sera d’autant plus proche de FB que la mesure de l’angle 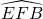sera petite.

Explications :

i) On considère la triangle AFE :
. Or . Donc , soit .

On considère la triangle ADF :
. Or . Donc . Comme , il vient . D’où .

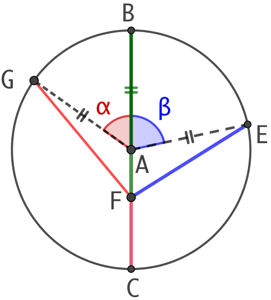ii) Supposons que G est plus près de B que E.

Alors et .

Or, Les triangles AGF et AFE ont chacun un côté de même longueur : et un côté commun AF.

Donc d’après la proposition I.24, .

Remarque : Il s’agit de la proposition III.7 des Éléments d’Euclide.