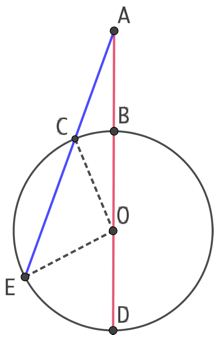
 Soient un cercle de centre O et un point quelconque A extérieur au cercle. La droite (OA) coupe le cercle aux points B et D. Soit un point quelconque C du cercle. La droite (AC) coupe le cercle au point E. Alors
Soient un cercle de centre O et un point quelconque A extérieur au cercle. La droite (OA) coupe le cercle aux points B et D. Soit un point quelconque C du cercle. La droite (AC) coupe le cercle au point E. Alors ![]() et
et ![]() .
.
Explications :
On considère le triangle ACO : ![]() . (1)
. (1)
Or ![]() et
et ![]() .
.
Donc (1) devient : ![]() . En simplifiant il vient :
. En simplifiant il vient : ![]() .
.
On considère le triangle AEO : ![]() . (2)
. (2)
Or ![]() dont
dont ![]()
Ainsi (2) devient : ![]() .
.
Remarque : Il s’agit de la partie principale de la proposition III.8 des Éléments d’Euclide.
