Une construction du nombre d’or se trouve dans l’article Le nombre d’or.
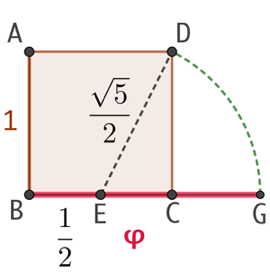 Construction n°1 :
Construction n°1 :
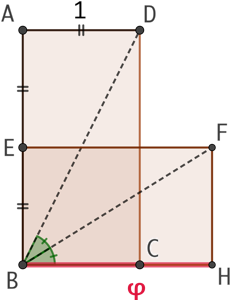 Construction n°2 :
Construction n°2 :
- On trace un rectangle ABCD de dimensions 1 et 2.
- On place le point E milieu de [AB].
- On trace la droite perpendiculaire à (AB) passant par E.
- On trace la bissectrice de l’angle
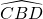 . Cette bissectrice rencontre la droite perpendiculaire à (BC) au point F.
. Cette bissectrice rencontre la droite perpendiculaire à (BC) au point F. - On trace la droite perpendiculaire à (EF) passant par F. Elle coupe la droite (BC) en H.
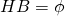 .
.
Explications :
Posons ![]() . Alors
. Alors ![]() .
.
![]() . (1)
. (1)
Par ailleurs ![]() .
.
Donc (1) s’écrit après simplification : ![]() soit
soit ![]() , c’est-à-dire :
, c’est-à-dire : ![]() .
.
En divisant par ![]() , on obtient :
, on obtient : ![]() . C’est-a-dire :
. C’est-a-dire : ![]() (2).
(2).
La racine positive de l’équation (2) est ![]() , donc
, donc ![]() puisque
puisque ![]() .
.
