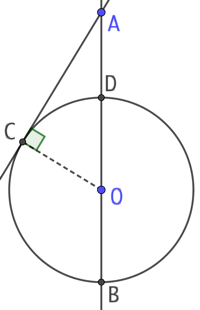
 Étant donné un cercle de centre O et un point A n’appartenant par au cercle, on trace la tangente au cercle passant par A et la droite (AO). La tangente rencontre le cercle en C et les deux points d’intersection de (AO) et du cercle sont B et D. On démontre que
Étant donné un cercle de centre O et un point A n’appartenant par au cercle, on trace la tangente au cercle passant par A et la droite (AO). La tangente rencontre le cercle en C et les deux points d’intersection de (AO) et du cercle sont B et D. On démontre que ![]() ainsi :
ainsi :
(AC) est la tangente au cercle en C donc les droite (OC) et (AC) sont perpendiculaires, donc ![]() .
.
![]() puisque
puisque ![]() .
.
Donc ![]() .
.
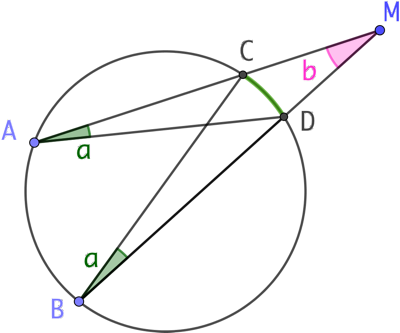 Remarque : Il s’agit d’un cas particulier de calcul de puissance d’un point par rapport à un cercle. C’est la situation extrême où les points A et C sont confondus.
Remarque : Il s’agit d’un cas particulier de calcul de puissance d’un point par rapport à un cercle. C’est la situation extrême où les points A et C sont confondus.
Remarque : la réciproque est exacte. Dans les conditions identiques, si ![]() alors la droite (AC) sera tangente au cercle en C.
alors la droite (AC) sera tangente au cercle en C.
Autre formulation pour la puissance d’un point :
Soient ![]() le rayon du cercle et
le rayon du cercle et ![]() . Alors la puissance du point A par rapport au cercle de centre O et de rayon
. Alors la puissance du point A par rapport au cercle de centre O et de rayon ![]() est :
est : ![]()
Remarque : Il s’agit des propositions III.36 et III.37 des Éléments d’Euclide.
