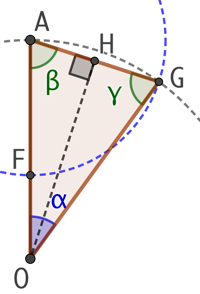
 Euclide a proposé pour le triangle d’or (qu’il ne nomme pas) la construction suivante :
Euclide a proposé pour le triangle d’or (qu’il ne nomme pas) la construction suivante :
- On trace un segment [OA].
- On place le point F tel que le carré de côté AF et le rectangle de côtés OF et OA aient la même aire (voir Partage d’un segment en deux pour construire un carré et un rectangle de même aire)
- On trace le cercle de centre O et de rayon OA.
- On trace le cercle de centre A et de rayon AF.
- Ces deux cercles se coupent en G. Le triangle OGA est un triangle d’or.
Explications :
Si on prend ![]() , alors
, alors ![]() .
.
Soit H le milieu de [AG]. Alors ![]() .
.
![]() donc
donc ![]() . Voir Triangle d’or.
. Voir Triangle d’or.
Par construction ![]() donc
donc ![]() et
et ![]() .
.
Remarque : Il s’agit de la proposition IV.10 des Éléments d’Euclide.
