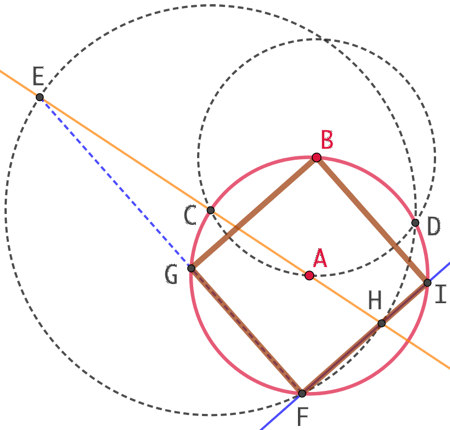
L’objectif est de construire un carré inscrit dans un cercle donné.
Construction :
Soit le cercle de centre A passant par B.
- On trace le cercle de centre B passant par A.
- Les deux cercles se coupent aux points C et D.
- On trace le cercle de centre C passant par D. Ce cercle coupe le cercle de centre A en F.
- On trace la droite (AC). Elle coupe le cercle de centre C en E et en H.
- On trace la droite (EF). Elle coupe le cercle de centre A en G.
- On trace la droite (FH). Elle coupe le cercle de centre A en I.
- BGFI est un carré inscrit dans le cercle de centre A.
Explications :
EH est un diamètre du cercle de centre C et F est sur ce cercle donc EFH est un triangle rectangle en F.
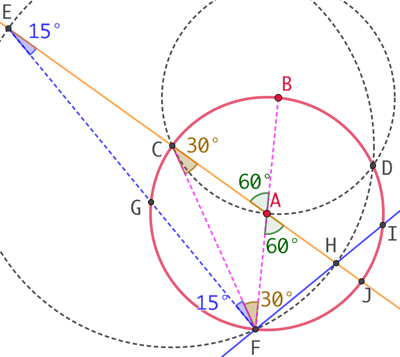BF est un diamètre du cercle de centre A et I est sur ce cercle donc BFI est un triangle rectangle en I. De même BGF est un triangle rectangle en G.
Donc le quadrilatère BGFI possède trois angles droits. C’est un rectangle.
Par construction, le triangle ABC est équilatéral. Donc 
car ces deux angles sont opposés par le sommet.
Dans le cercle de centre A : 
. comme angle inscrit et angle au centre. On note que 
Dans le cercle de centre C : 
comme angle inscrit et angle au centre. On note que 
.
CEF est un triangle isocèle car les points E et F sont situés sur le cercle de centre C. Donc 
.
CAF est un triangle isocèle car les points C et F sont situés sur le cercle de centre A. Donc 
.
Par conséquent 
. On note que 
.
Dans le triangle BGF rectangle en G : Si 
alors 
. Donc le triangle BFG est aussi isocèle, c’est-à-dire que 
.
Conclusion : puisque le rectangle BGFI a deux côtés consécutifs de même longueur, c’est donc un carré.
