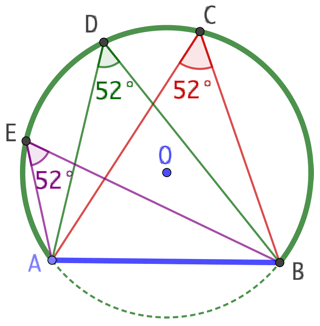
Étant donné un segment, quel est le lieu géométrique des points, faisant avec les deux extrémités de ce segment, un angle de mesure donnée ?
Réponse : il s’agit d’un arc de cercle qui a pour corde le segment donné et pour centre le point de la médiatrice du segment faisant avec les extrémités du segment un angle de mesure double de celle donnée.
Explications :
Soit un segment [AB] et une mesure d’angle 
.
Soit le point O appartenant à la médiatrice de [AB] et tel que 
et Alors 
. Soit alors 
, le cercle de centre O et passant par A et B.
Soit un point C tel que 
. Supposons que 
.(raisonnement par l’absurde).
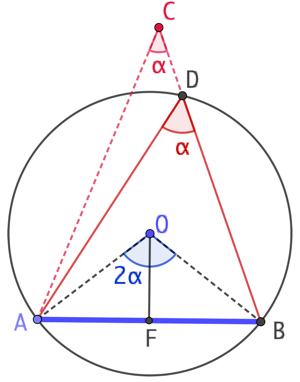Soit alors D l’intersection de la droite (CB) avec . D’après la propriété de l’angle inscrit et de l’angle au centre, on sait que 
, ce qui est contradictoire avec l’hypothèse que .
Donc 
.
Voir : Angle à l’intérieur d’un triangle
