Centre d’une similitude directe

Étant donnés les points A, B, A', B', le centre de la similitude directe s telle que A'=s(A) et B'=s(B), s’obtient de la façon suivante :

Construction du centre de la similitude :

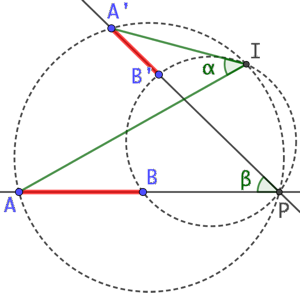
  • On place le point P intersection des droites (AB) et (A’B’).
  • On trace le cercle passant par les points A, A’ et P.
  • On trace le cercle passant par B, B’ et P.
  • Le deuxième point d’intersection des deux cercles est I, centre de la similitude s.

Explications :

Par construction les points A, A’, P et I sont cocycliques donc \widehat{A'PA} = \widehat{A'IA} = \beta.

Par construction les points B, B’, P et I sont cocycliques donc \widehat{B'PB} = \widehat{B'IB} = \beta.

Donc \widehat{A'IA} = \widehat{B'IB}. On en conclut que I est le centre de la similitude.

Pour s’en convaincre, supposons que la similitude s soit définie par s(z) = uz +v et soient a, a’, b et b’, les affixes respectifs des points A, A’, B, B’. On peut alors écrire : a' = ua +v et b' = ub + v. Donc \dfrac{b' - a'}{b - a} = u, ce qui implique que \arg \dfrac{b' - a'}{b - a} est constant et égal à \widehat{\overrightarrow{AB}, \overrightarrow{A'B}}.

or \widehat{\overrightarrow{AB}, \overrightarrow{A'B}} = \widehat{\overrightarrow{IA'}, \overrightarrow{IA}}. Ainsi l’image de I par la similitude s est I. I est le point invariant donc le centre de la similitude s.

Print Friendly, PDF & Email