Étant donné un segment [AB], le lieux géométrique des points dont les droites joignant ces points aux extrémités de [AB] forment des angles de mesure constante 
, est un arc de cercle allant de A à B.
Explications :
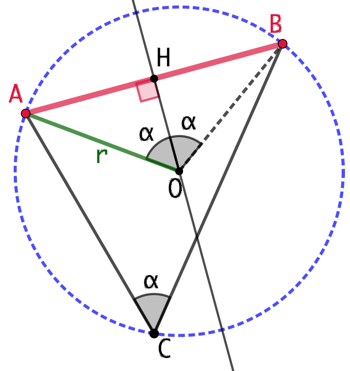
Soit C un point tel que 
. Par trois points donnés, il passe un cercle unique qui est le cercle circonscrit au triangle ABC. Soient O le centre de ce cercle et 
son rayon.
D’après le théorème de l’angle au centre, 
. Soit (OH) la médiatrice de [AB]. Le triangle OAB est isocèle en O donc (OH) est également la bissectrice de l’angle 
.
, ce qui donne 
.
Ainsi le rayon du cercle circonscrit ne dépend que de la longueur AB et de l’angle . Il ne dépend pas de la position du point C.
Soit D un autre point tel que 
. Alors, d’après ce qui précède, D appartient à un cercle de rayon . Soit 
le centre de ce cercle. appartient à la médiatrice de [AB], c’est-à-dire (OH). Comme 
, nécessairement, 
.
Ce qui démontre que C et D appartiennent à l’arc de cercle de centre O, de rayon et d’extrémités A et B.
