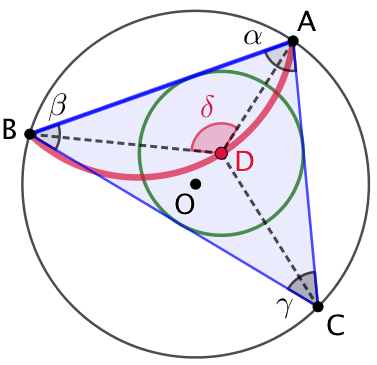
Centres des cercles inscrits dans des triangles inscrits dans un cercle

Soit un cercle de centre O et [AB] une corde de ce cercle. Soit C un point de ce cercle. On construit le cercle inscrit dans le triangle ABC. Quand le point C décrit l’un des deux arcs de cercle délimité par la corde [AB], le centre du cercle inscrit dans ABC décrit un arc de cercle également délimité par la corde [AB].

Explications :

Posons \widehat{ACB} = \gamma. En vertu du théorème de l’angle inscrit, \gamma reste contant quand C parcourt l’arc de cercle AB.

Soit D le centre du cercle inscrit dans le triangle ABC. D est le point d’intersection des trois bissectrices de ABC. Posons \widehat{BAC} = \alpha et \widehat{CBA} = \beta.

Alors \delta = \pi - \left ( \dfrac{\alpha}{2} + \dfrac{\beta}{2} \right ) = \pi - \dfrac{\alpha + \beta}{2} = \pi- \dfrac{\pi - \gamma}{2} = \dfrac{\pi + \gamma}{2}.

Comme \gamma est constant, il vient que \delta est aussi constant. C’est-à-dire que le point D voit la corde [AB] sous un angle constant. En appliquant la réciproque du théorème de l’angle inscrit, on en conclut que D décrit un arc de cercle d’extrémité [AB].

Print Friendly, PDF & Email