 L’axe radical de deux cercles distincts est lieu géométrique des points dont les puissances aux deux cercles sont égales.
L’axe radical de deux cercles distincts est lieu géométrique des points dont les puissances aux deux cercles sont égales.
Avant de pouvoir le construire, il faut faire le calcul préliminaire :
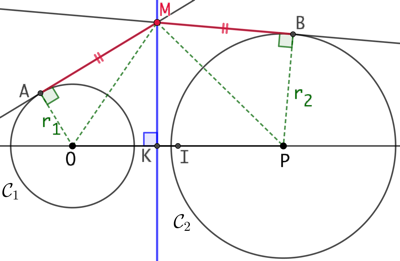
Soient deux cercles et
de centres O et P, de rayons
et
, M un point de l’axe radical de ces deux cercles, (MA) la tangente en
passant par M et (MB) la tangente en
passant par M.
En utilisant le théorème de Pythagore pour les triangles MAO et MBP, on obtient : et
.
Les puissances de M par rapport à ces deux cercles sont égales : . Ce qui donne :
, soit
. (1)
Construction : L’égalité (1) s’interprète ainsi : l’axe radical est le lieu géométrique des points dont les carrés des distances à deux points fixes (O et P) font entre eux un différence constante (). Voir : Lieux géométriques des points dont les carrés des distances à deux points fixes ont une différence constante.
Suite du calcul : Soit K le projeté orthogonal de M sur (OP). En appliquant le théorème de Pythagore aux triangles MOK et MPK, on obtient : et
.
En remplaçant dans (1) : , soit
. Comme
, il vient :
. (2)
Ainsi ne dépend pas de K et est constant. Tous les points de la droite passant par K et perpendiculaire à (OP) ont le même projeté orthogonal K. On en conclut que l’axe radical est cette droite passant par K et perpendiculaire à (OP).
Sachant que , l’égalité (2) devient :
Soit I le milieu de [OP], on obtient .
Si le alors l’axe radical est à gauche du milieu de [OP].
Remarque : Il existe deux positions du point M pour lesquelles les tangentes (MA) et (MB) sont confondues et pour lesquelles M est le milieu de [AB]. Un autre procédé de construction consiste à tracer ces deux tangentes communes aux deux cercles. Alors l’axe radical est la droite passant par les deux milieux. Voir : Tangente commune à deux cercles.
