I – Périmètre et aire d’une figure
- Le périmètre d’une figure est la mesure de la longueur de son contour, exprimée dans une unité de longueur donnée.
- L’aire d’une figure est la mesure de sa surface, exprimée dans une unité d’aire donnée.
 Exemple :
Exemple :
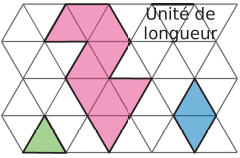
Le périmètre de la figure rose : on compte le nombre d’unités de longueur qui permettent de mesurer la longueur de son contour. Le périmètre de la figure rose est donc de 11 unités de longueur.
L’aire de la figure rose si on prend pour unité d’aire l’aire du triangle vert : On compte le nombre d’unités d’aire qui la constituent. La figure rose est constituée de 9 triangles. Son aire est donc de 9 triangles verts.
L’aire de la figure rose si on prend pour unité d’aire l’aire du losange bleu : Elle est également constituée de 4,5 losanges. Son aire est donc de 4,5 losanges bleus.
ATTENTION : les mesures dépendent des unités de mesure choisies pour exprimer des longueurs ou des aires.
- Deux figures non superposables peuvent avoir le même périmètre.
- Deux figures non superposables peuvent avoir la même aire.
- Des figures peuvent avoir la même aire mais des périmètres différents.
- Des figures peuvent avoir le même périmètre mais des aires différentes.
Exemples :
 |
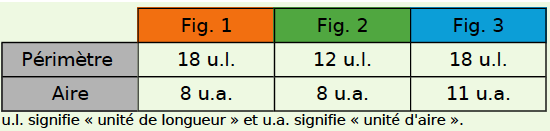 |
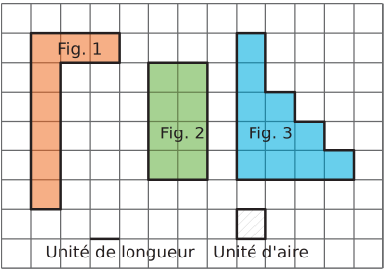
Les figures 1 et 2 ont la même aire mais elles n’ont pas le même périmètre.
Les figures 1 et 3 ont le même périmètre mais elles n’ont pas la même aire.
II – Unités d’aire
- L’unité d’aire usuelle est le mètre carré (noté m2) qui représente l’aire d’un carré de côté 1 mètre.
- On utilise aussi : ses multiples (dam2, hm2, km2) et ses sous-multiples (dm2, cm2, mm2).
 Exemple :
Exemple :
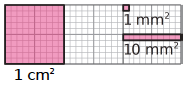
- 1 cm2 est l’aire d’un carré d’un centimètre de côté.
- 1 mm2 est l’aire d’un carré d’un millimètre de côté.
- Dans 1 cm2, il y a 100 mm2.
Remarque : L’aire d’un terrain se mesure souvent en hectare, noté ha, qui est égal à un hm2. Donc 1 ha = 10 000 m2.
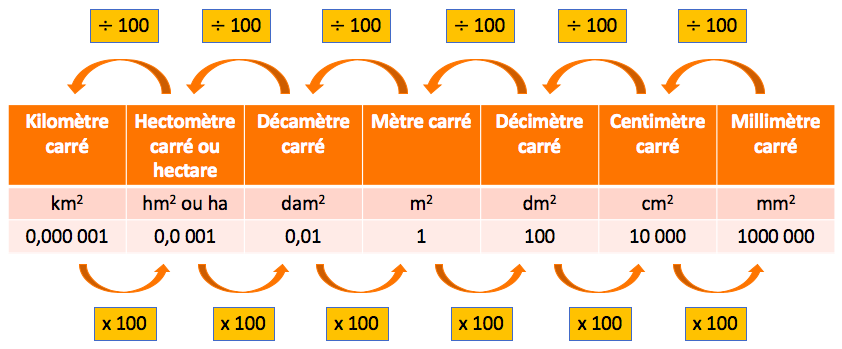
Exemples :
- 53 dam2 = 5 300 m2
- 7,81 ha = 781 dam2 = 78 100 m2
- 5 dm2 = 0,05 m2
- 8 000 cm2 = 0,8 m2
III – Périmètre et aire de figures usuelles
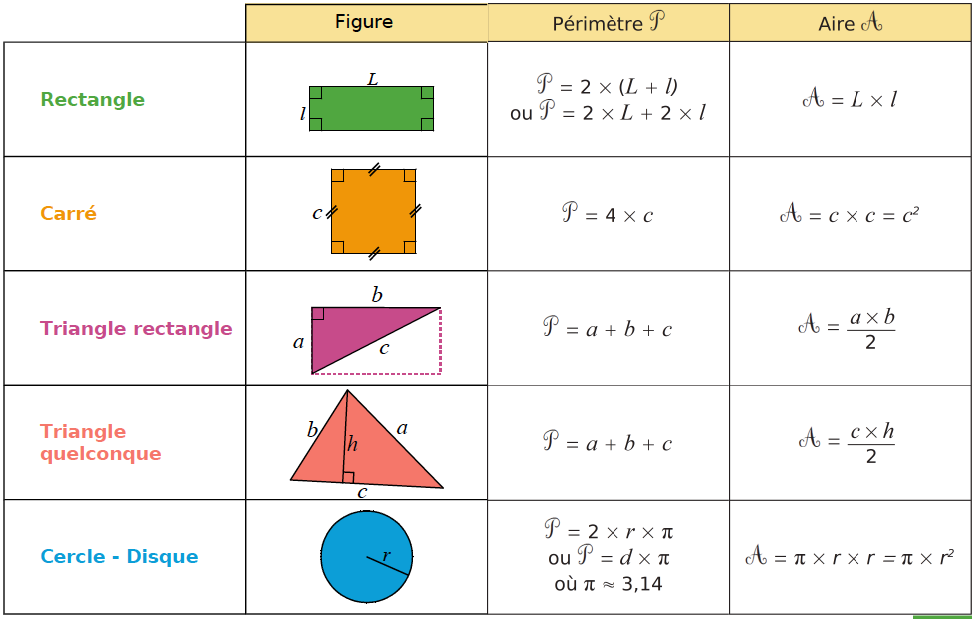
IV – Calculs de périmètres et d’aires de figures composées
 À partir des formules des périmètres et des d’aires de figures usuelles, il est possible de calculer les périmètres et les aires de figures plus compliquées, dans lesquelles on peut retrouver les figures usuelles.
À partir des formules des périmètres et des d’aires de figures usuelles, il est possible de calculer les périmètres et les aires de figures plus compliquées, dans lesquelles on peut retrouver les figures usuelles.
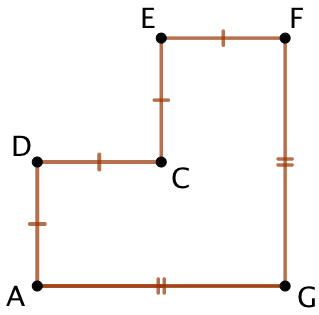
Exemple : Calcul du périmètre de la figure ci-contre, sachant que AD = 3,5 cm et AG = 7 cm
En observant le codage de la figure, on déduit les autres longueurs : DC = CE = EF = AD = 3,5 cm et FG = AG = 7 cm.
Par conséquent le périmètre est : ![]() cm.
cm.
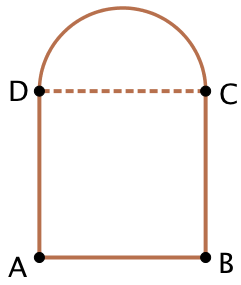 Exemple : Calcul de l’aire du jardin ci-contre composé d’un carré ABCD et d’un demi-disque de diamètre CD égal à 6 m. On prendra
Exemple : Calcul de l’aire du jardin ci-contre composé d’un carré ABCD et d’un demi-disque de diamètre CD égal à 6 m. On prendra ![]() .
.
La longueur des côtés du carré ABCD est 6 m. Donc l’aire du carré sera : ![]() m2.
m2.
Le rayon du demi-disque est la moitié de DC : ![]() cm.
cm.
Si le disque était entier, son aire serait : ![]() . Comme nous n’avons qu’un demi-disque, son aire sera de
. Comme nous n’avons qu’un demi-disque, son aire sera de ![]() m2.
m2.
Conclusion : l’aire du jardin est ![]() m2.
m2.
V – Volume d’un solide
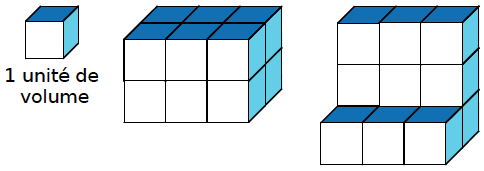 Exemple : Pour trouver le volume de chaque solide, il suffit de compter le nombre d’unités de volume qui le constituent. Les deux solides ont pour volume 12 (en unités de volume) alors qu’ils n’ont pas la même forme.
Exemple : Pour trouver le volume de chaque solide, il suffit de compter le nombre d’unités de volume qui le constituent. Les deux solides ont pour volume 12 (en unités de volume) alors qu’ils n’ont pas la même forme.
VI – Unités de volume et de capacité
1) Unités de volume
Exemples :
- 1 cm3 est le volume d’un cube d’un centimètre de côté.
- 1 mm3 est le volume d’un cube d’un millimètre de côté.
- Dans 1 cm3, il y a 1 000 mm3.
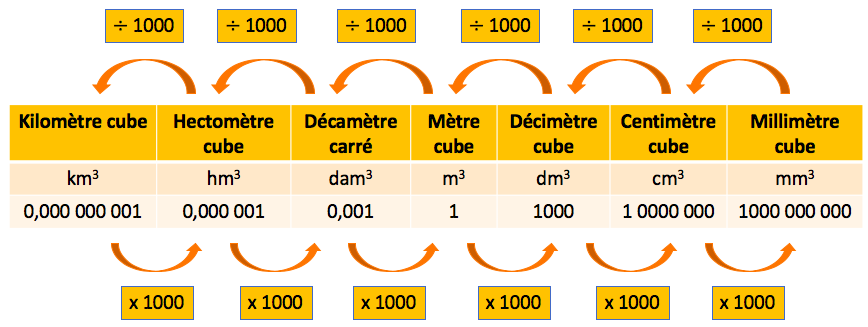
Exemples :
- 53 dam3 = 53 000 m3
- 0,36 m3 = 360 dm3
- 5 dm3 = 0,005 m3
Autres unités fréquemment utilisées : Pour mesurer des volumes de liquide, on utilise :
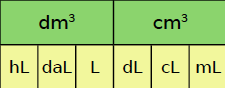 le litre : 1 L = 1 dm3
le litre : 1 L = 1 dm3- l’hectolitre : 1 hL = 100 L
- le décilitre : 1 dL = 100 cm3
- le centilitre : 1 cL = 10 cm3
- le millilitre : 1 mL = 1 cm3
Exemples :
- 15 L = 0,15 hL
- 3,5 L = 350 cL
- 3 mL = 0,3 cL
