I – Vocabulaire
![]() Exemple : On considère le nombre décimal 1 345,824.
Exemple : On considère le nombre décimal 1 345,824.
On peut utiliser un tableau pour représenter ce nombre :

Ce nombre peut se lire de trois manières différentes :
- mille-trois-cent-quarante-cinq unités et huit−cent−vingt−quatre millièmes
- mille-trois-cent-quarante-cinq unités et huit dixièmes deux centièmes quatre millièmes
- mille-trois-cent-quarante-cinq unités virgule huit−cent−vingt−quatre
Voici le nom de chaque chiffre :
- 1 est le chiffre des unités des milliers
- 3 est le chiffre des centaines
- 4 est le chiffre des dizaines
- 5 est le chiffre des unités
- 8 est le chiffre des dixièmes
- 2 est le chiffre des centièmes
- 4 est le chiffre des millièmes
II – Comparaison
- on compare les parties entières ;
- si les parties entières sont égales alors on compare les chiffres des dixièmes ;
- si les chiffres des dixièmes sont égaux alors on compare les chiffres des centièmes ;
- et ainsi de suite jusqu’à ce que les deux nombres aient des chiffres différents.
Exemple : On veut comparer les nombres 81,357 et 81,36.
- On compare d’abord les parties entières des deux nombres ;
- elles sont égales donc on compare les chiffres des dixièmes ;
- ils sont égaux donc on compare les chiffres des centièmes ;
- 5 < 6 donc 81,357 < 81,36.
III – Addition
- Les nombres que l’on additionne s’appellent les termes.
- Le résultat d’une addition s’appelle la somme.
Dans une addition, on a le droit de :
- regrouper les termes ;
- changer des termes de place.
Exemple : Comment calculer astucieusement 46 + 37 + 54 + 63 ?
46 + 37 + 54 + 63 = (46 + 54) + (37 + 63) = 100 + 100 = 200
IV – Soustraction
- Les nombres que l’on soustrait s’appellent les termes.
- Le résultat d’une soustraction s’appelle la différence.
- On ne peut pas changer les termes de place dans une soustraction.
- Dans un calcul ne comportant que des additions et des soustractions, on effectue les opérations l’une après l’autre en commençant par la gauche.
Exemple : on veut calculer ![]()
- On commence par la soustraction :
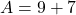 .
. - Puis on s’occupe de l’addition :
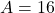
Exemple : On veut calculer ![]()
- On commence par l’addition :
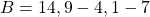
- On poursuit avec la première soustraction :
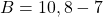
- On termine avec la seconde soustraction :
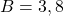
V – Multiplication
- Les nombres que l’on multiplie s’appellent les facteurs.
- Le résultat d’une multiplication s’appelle le produit.
Exemple : Comment calculer astucieusement 4 × 56 × 25 ?
4 × 56 × 25 = (4 × 25) × 56 = 100 × 56 = 5 600
VI – Division
Exemple : Quand je divise 12 par 4, 12 est le dividende et 3 le diviseur. ![]() , donc le quotient de la division de 12 par 4 est 3.
, donc le quotient de la division de 12 par 4 est 3.
Remarques :
- Le quotient de 12 par 4 est égal à 3. C’est un nombre entier.
- Le quotient de 17 par 4 est égal à 3,75. C’est un nombre décimal.
- Le quotient de 2 par 3 ne tombe pas juste. Ce n’est pas un nombre décimal.
Dans ce cas, on peut écrire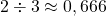 . Mais 0,666 est une valeur approchée de ce quotient.
. Mais 0,666 est une valeur approchée de ce quotient.
Exemple : On veut calculer ![]()
- On commence par la division :
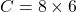
- Puis on passe à la multiplication :
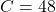
VII – Toutes les opérations
Exemple : On veut calculer ![]()
- La multiplication est prioritaire par rapport à la soustraction. On commence donc par la multiplication :
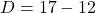
- Puis on s’occupe de la soustraction :
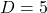
Exemple : On veut calculer ![]()
- La multiplication et la division sont prioritaires. On commence par elles :
- On s’occupe des deux soustractions en commençant par la première :
VIII – Les parenthèses
Puis à l’intérieur des parenthèses, on effectue les calculs en respectant les priorités et toutes les règles de calcul annoncées précédemment.
Exemple : On veut calculer ![]()
- On commence par l’addition dans la parenthèse :
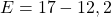
- Puis on fait la soustraction :
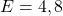
Exemple : On veut calculer ![]()
- On commence par les opérations à l’intérieur des parenthèses :
- Puis on termine par la multiplication :
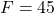
Exemple : On veut calculer ![]()
Cet exemple comporte deux niveaux de parenthèses : des parenthèses à l’intérieur de crochets qui jouent le même rôle que des parenthèses. La règle est de commencer par les parenthèses les pus intérieures. Donc, dans cet exemple, on commence par le calcul à l’intérieur des parenthèses puis le calcul restant à l’intérieur des crochets.
- On commence par le calcul à l’intérieur des parenthèses :
![Rendered by QuickLaTeX.com G = 8 - [12 \times 0,5]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-f614b958df95c5ef3ee0d399977f3650_l3.png)
- On continue par le calcul restant à l’intérieur des crochets :
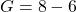 .
. - On termine par la soustraction :
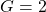
IX – Ordre de grandeur
Remarque : Calculer un ordre de grandeur permet de vérifier plus facilement la cohérence d’un résultat, c’est-à-dire que ce résultat est logique par rapport à l’énoncé du problème.
Exemple : La superficie de la France métropolitaine est de 551 695 km2. Un ordre de grandeur de cette superficie est 550 000 km2. Cet ordre de ordre de grandeur n’est pas la valeur exacte de la superficie de la France métropolitaine mais est une valeur suffisamment proche pour être utilisée dans des calculs.
Exemple : On veut déterminer un ordre de grandeur du calcul suivant : 546,3 + 52.
On cherche un ordre de grandeur de chaque terme qu’on utilise dans le calcul.
550 est proche de 546,3 et 50 est proche de 52. Comme 550 + 50 = 600, la somme 546,3 + 52 est proche de 600. On dit que 600 est un ordre de grandeur de 546,3 + 52.
Exemple : On veut déterminer un ordre de grandeur du calcul suivant : 65,7 × 4,1
On cherche un ordre de grandeur de chaque facteur qu’on utilise dans le calcul.
65,7 est proche de 65 et 4,1 est proche de 4. Comme 65 × 4 = 260, le produit 65,7 × 4,1 est proche de 260. 260 est donc un ordre de grandeur de 65,7 × 4,1.
X – Encadrement d’un nombre décimal
Exemples :
- 2,4 est encadré par 2 et par 3 car 2 < 2,4 < 3
- 3,141 est encadré par 3,14 et par 3,15 car 3,14 < 3,141 < 3,15
- Encadrement à l’unité : la différence entre le plus grand et le plus petit vaut 1.
- Encadrement au dixième : la différence entre le plus grand et le plus petit vaut 0,1.
- Encadrement au centième : la différence entre le plus grand et le plus petit vaut 0,01.
- Encadrement au millième : la différence entre le plus grand et le plus petit vaut 0,001.
- etc …
Exemples :
- Encadrement à l’unité : 2 < 2,4 < 3
- Encadrement au centième : 3,14 < 3,141 < 3,15
Exemple : entre 9,81 et 9,82, je peux intercaler 9,813 car : 9,81 < 9,813 < 9,82.
EXERCICES
- 2, 3 et 4 / 9 : calcul
- 5 / 9 : traduction d’un texte en expression numérique
- 6 / 9 : ordre de grandeur
- 7, 8 / 9 : calcul avec parenthèses
- 10 / 9 : Le compte est bon
- 15 / 10 : traduction d’un texte en expression numérique avec ordre de grandeur
- 19 / 10 : Recherche de nombres connaissant un résultat
- 20 / 10 : Petits problèmes de calcul
- 28 / 11 : Trouver les signes opératoires
- 29 / 11 : calcul astucieux
- 32 / 11 : calcul par étape
- 35 / 12 : petits problèmes
- 39 / 12 : calculs avec parenthèses
- 41 / 12 : ordre de grandeur
- 42 / 12 : calcul avec deux niveaux de parenthèses
- 43 / 12 : replacer des parenthèses
- 59 / 14 : nombre à découvrir
- 62 / 14 : calcul de distance
- 65 / 15 : écologie
- 67 / 16 : traduction d’un texte en expression numérique
- 72 / 16 : le compte est bon
