I – Expression littérale
Exemples :
- L’aire d’un carré de côté
 s’exprime avec l’expression littérale :
s’exprime avec l’expression littérale : 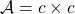 . On dit que l’aire du carré s’exprime en fonction de
. On dit que l’aire du carré s’exprime en fonction de  .
. - Le triple du nombre
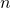 s’exprime sous la forme :
s’exprime sous la forme : 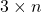 .
.
Exemple : Le périmètre d’un rectangle de longueur ![]() et de largeur
et de largeur ![]() est :
est : ![]() .
.
Remarques :
• On peut simplifier les écritures : ![]() en
en ![]() et
et ![]() en
en ![]() .
.
• ATTENTION : On ne peut pas supprimer le symbole de multiplication ![]() entre deux nombres :
entre deux nombres : ![]() ne peut pas s’écrire
ne peut pas s’écrire ![]() .
.
- Le carré de
 est le produit
est le produit 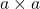 et est noté :
et est noté : 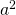 .
. - Le cube de
 est le produit
est le produit 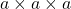 et est noté :
et est noté : 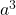 .
.
Exemples :
- L’aire d’un carré de côté c est : c2.
- Le volume d’un cube d’arête c est = c3.
II – Évaluer une expression littérale
Exemple : Soit l’expression littérale : ![]() . Quelle est la valeur obtenue pour B quand on donne plusieurs valeurs différentes à
. Quelle est la valeur obtenue pour B quand on donne plusieurs valeurs différentes à ![]() ?
?
- Si
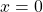 , alors
, alors 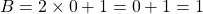
- Si
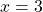 alors
alors 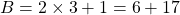
- Si
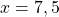 alors
alors 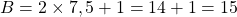 .
.
 Essayons de comprendre ce que représente l’expression littérale
Essayons de comprendre ce que représente l’expression littérale ![]() par un petit algorithme :
par un petit algorithme :
III – Égalité de deux expressions littérales
Exemple : On se propose de tester l’égalité suivante : ![]() pour
pour ![]() , puis pour
, puis pour ![]()
- Pour
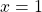 :
:
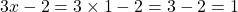 et
et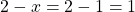 .
.- Conclusion : pour
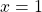 , les deux expressions sont égales.
, les deux expressions sont égales.
- Pour
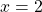 :
:
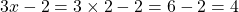 et
et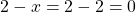 .
.- Conclusion : pour
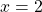 , les deux expressions ne sont pas égales.
, les deux expressions ne sont pas égales.
IV – Produire une expression numérique
Exemple : Étant donné un nombre ![]() quelconque, déterminer l’expression correspondant à la phrase suivante : soustraire le double de
quelconque, déterminer l’expression correspondant à la phrase suivante : soustraire le double de ![]() au carré de
au carré de ![]() .
.
Le carré de ![]() est :
est : ![]() . Le double de
. Le double de ![]() est :
est : ![]() . Donc l’expression recherchée est :
. Donc l’expression recherchée est : ![]() .
.
Exemple : Paul possède 17 € pour acheter des fleurs à sa maman. Il choisit des roses coûtant 3,50 € pièce. Si le nombre de fleurs achetées par Paul est représenté par la lettre ![]() , quelle est l’expression qui donne la somme d’argent qu’il reste à Paul après son achat ?
, quelle est l’expression qui donne la somme d’argent qu’il reste à Paul après son achat ?
- Chaque fleur coûte 3,50 €, donc
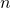 fleurs coûtent
fleurs coûtent 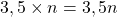 .
. - Paul possède 17 €. Après son achat, il lui reste :
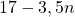 euros.
euros. - Par exemple, s’il achète 4 fleurs, il lui restera :
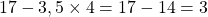 .
.
V – Distributivité

2 pommes + 3 pommes = 5 pommes.
On remplace la pomme par la lettre a. Sur le modèle des pommes, on peut alors écrire cette égalité : 2a + 3a = 5a. (1)
On sait évidemment que 5 = 2 + 3. Donc 5a = (2 + 3)a. Alors l’égalité (1) s’écrit aussi : 2a + 3a = (2 + 3)a.
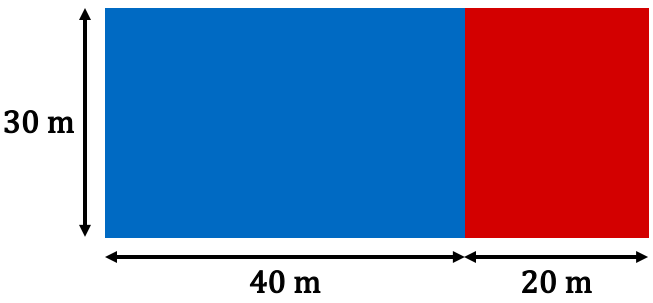 Voici un champ composé de deux parcelles dont les dimensions sont précisées. On peut calculer l’aire totale de ce champ de deux façons différentes.
Voici un champ composé de deux parcelles dont les dimensions sont précisées. On peut calculer l’aire totale de ce champ de deux façons différentes.
1er calcul : on calcule l’aire de chaque parcelle puis on fait la somme des deux aires.
- La parcelle bleue :
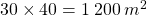 .
. - La parcelle rouge :
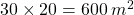 .
. - L’aire du champ :
2ème calcul : la longueur totale du champ est : ![]() . Par conséquent son aire est :
. Par conséquent son aire est : ![]() .
.
Conclusion : ![]()
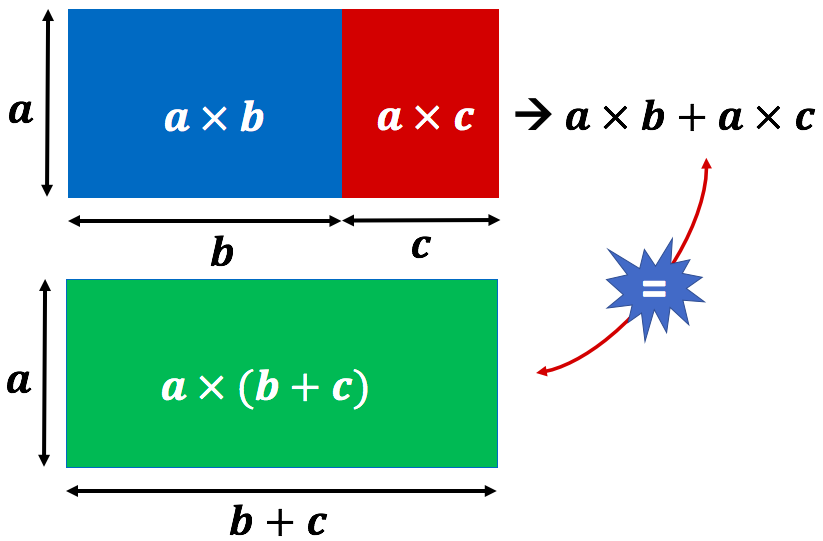 Remplaçons les nombres par des lettres.
Remplaçons les nombres par des lettres.
On peut écrire le même genre d’égalité :
![]()
Cette égalité est une propriété qui s’appelle la distributivité de la multiplication par rapport à l’addition.
