I – Somme des angles
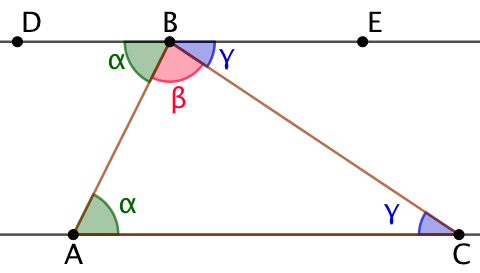 Démonstration : Soit un triangle ABC et ses trois angles
Démonstration : Soit un triangle ABC et ses trois angles ![]() et
et ![]() . On va démontrer que
. On va démontrer que ![]() °.
°.
Traçons la droite (DE), parallèle à la droite (AC) et passant par B. On utilise alors la propriété des angles alternes-internes :
Si deux angles alternes-internes sont déterminés par des droites parallèles, alors ils ont la même mesure.
Donc, on en déduit que :
Comme les points D, B et E sont lignés, l’angle ![]()
Mais ![]() .
.
Conclusion ![]() °.
°.
II – Milieu et médiatrice d’un segment
- Le milieu du segment [AB] est le point du segment [AB] qui est équidistant (à la même distance) des extrémités A et B.
- Dit autrement : Le milieu d’un segment coupe ce segment en deux segments de même longueur.
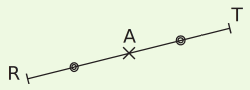 Exemple : Le point A est le milieu du segment [RT]. Cela signifie que les points A,R et T sont alignés et que les distances AR et AT sont égales.
Exemple : Le point A est le milieu du segment [RT]. Cela signifie que les points A,R et T sont alignés et que les distances AR et AT sont égales.
Codage du milieu : Pour indiquer sur une figure que deux segments ont la même longueur, on leur ajoute un même symbole (un petit disque noir dans cet exemple).
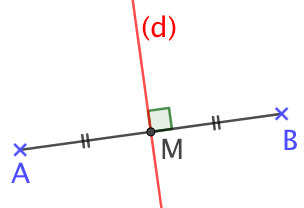 Exemple : La droite (d) est la médiatrice du segment [AB]. Elle passe par le point M, milieu du segment [AB]. Elle forme avec [AB] un angle droit.
Exemple : La droite (d) est la médiatrice du segment [AB]. Elle passe par le point M, milieu du segment [AB]. Elle forme avec [AB] un angle droit.
- Si un point appartient à la médiatrice d’un segment, alors il est équidistant des extrémités de ce segment.
- Si un point est équidistant des extrémités d’un segment, alors il appartient à la médiatrice de ce segment.
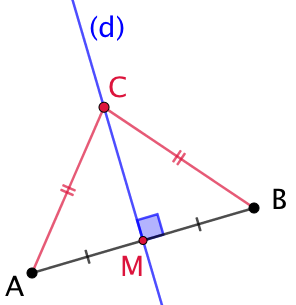 Exemple : Soit (d) la médiatrice du segment [AB].
Exemple : Soit (d) la médiatrice du segment [AB].
- Si le point C appartient (d), alors les distances CA et CB sont égales.
- Si CA = CB, alors C est un point de (d).
Construction de la médiatrice
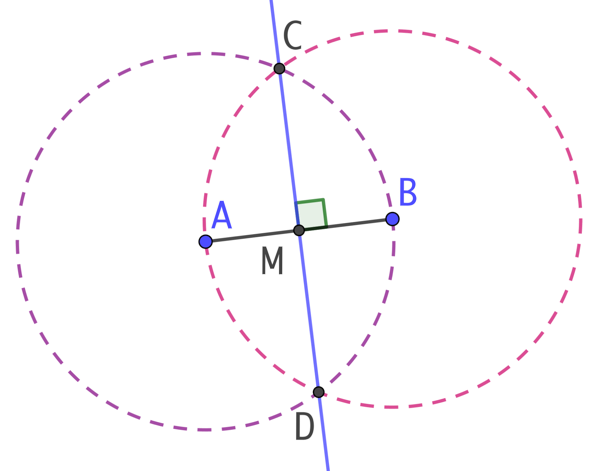 Pour tracer la médiatrice du segment [AB] :
Pour tracer la médiatrice du segment [AB] :
- On trace un cercle de centre A qui passe par B.
- On trace un cercle de centre B qui passe par A.
- Ces deux cercles se coupent aux points C et D.
- La droite (CD) est la médiatrice du segment [AB].
Pourquoi cette construction permet-elle d’obtenir la médiatrice ?
- Les deux cercles ont le même rayon AB.
- C appartient au cercle de centre A donc AC = AB.
- C appartient au cercle de centre B donc BC = AB.
- Par conséquent : AC = BC. Donc C est sur la médiatrice de [AB].
- Un même raisonnement permet de démontrer que D est sur la médiatrice de [AB].
- Ce qui permet de conclure que la droite (CD) est la médiatrice de [AB]
III – Médiatrices d’un triangle et cercle circonscrit
- Un triangle possède trois médiatrices puisqu’il possède trois côtés.
- Les médiatrices d’un triangle sont concourantes.
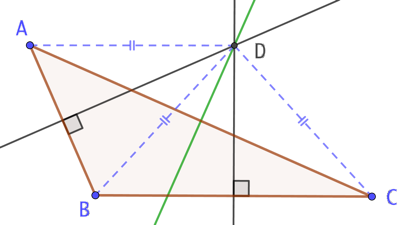 Démonstration : On va utiliser la propriété vue précédemment selon laquelle un point appartient à la médiatrice d’un segment s’il est équidistant des extrémités de ce segment.
Démonstration : On va utiliser la propriété vue précédemment selon laquelle un point appartient à la médiatrice d’un segment s’il est équidistant des extrémités de ce segment.
Soit un triangle ![]() . Nommons
. Nommons ![]() le point d’intersection des médiatrices des segments
le point d’intersection des médiatrices des segments ![]() et
et ![]() et démontrons que
et démontrons que ![]() appartient à la médiatrice de
appartient à la médiatrice de ![]() , en vert sur la figure.
, en vert sur la figure.
SI ![]() appartient à la médiatrice de
appartient à la médiatrice de ![]() alors
alors ![]() . Si
. Si ![]() appartient la médiatrice de
appartient la médiatrice de ![]() alors
alors ![]() .
.
Puisque ![]() et que
et que ![]() alors
alors ![]() . Cela permet donc d’affirmer que
. Cela permet donc d’affirmer que ![]() appartient à la médiatrice de
appartient à la médiatrice de ![]() . Conclusion : Les médiatrices de
. Conclusion : Les médiatrices de ![]() sont concourantes en
sont concourantes en ![]() .
.
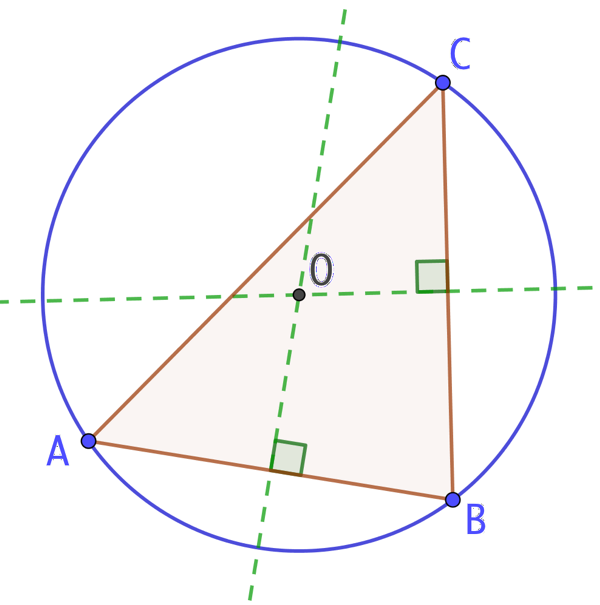 Exemple : le cercle circonscrit du triangle
Exemple : le cercle circonscrit du triangle ![]() est le cercle de centre
est le cercle de centre ![]() et de rayon
et de rayon ![]() . Le point
. Le point ![]() est le point d’intersection des médiatrices de
est le point d’intersection des médiatrices de ![]() .
.
Construction du cercle circonscrit :
- On construit deux médiatrices du triangle.
- Leur point d’intersection O est le centre du cercle circonscrit.
- On trace le cercle de centre O et passant par l’un des sommets du triangle.
