I – Losange
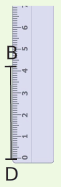
Exemple : On veut construire un losange ABCD tel que AB = 6 cm (un côté) et BD = 4,2 cm (une des deux diagonales).
 |
 |
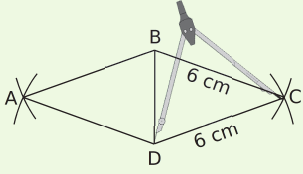 |
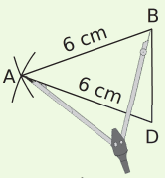
| On trace un segment [BD] de longueur 4,2 cm. | On construit un triangle ABD isocèle en A tel que AB = AD = 6 cm. | On construit le triangle CBD isocèle en C tel que CB = CD = 6 cm. |
Un losange possède donc toutes les propriétés d’un parallélogramme.
Démonstration : Par définition, un losange possède quatre côtés de même longueur, donc ses côtés opposés sont de même longueur. Comme ce n’est pas un quadrilatère croisé, on en déduit que c’est un parallélogramme.
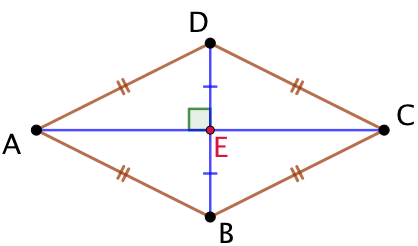 Démonstration : Soit ABCD est losange et E le milieu des deux diagonales. Nous allons démontrer que la droite (AC) est la médiatrice du segment [BD].
Démonstration : Soit ABCD est losange et E le milieu des deux diagonales. Nous allons démontrer que la droite (AC) est la médiatrice du segment [BD].
- Puisque AD = AB, le point A appartient à la médiatrice du segment [BD].
- Comme E est le milieu du segment [BD], il vient que la droite (AE) est la médiatrice du segment [BD]. Ce qui prouve que les droites (AE) et (BD) sont perpendiculaires.
- Par ailleurs E est aussi le milieu du segment [AC], donc la droite (AE) et la droite (AC) sont confondues.
- Finalement il vient que les droites (AC) et (BD), c’est-à-dire, les deux diagonales du losange, sont perpendiculaires.
Savoir reconnaître un losange
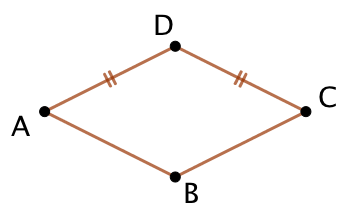 Démonstration : Soit un parallélogramme ABCD tel que AD = DC.
Démonstration : Soit un parallélogramme ABCD tel que AD = DC.
- ABCD est un parallélogramme donc ses côtés opposés ont la même longueur.
- Ainsi AD = BC et DC = AB. Mais comme AD = DC, on en déduit que les quatre côtés ont la même longueur.
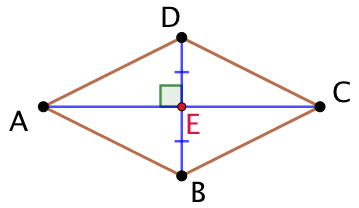 Démonstration : Soit un parallélogramme ABCD tel que ses diagonales (AC) et (DC) soient perpendiculaires.
Démonstration : Soit un parallélogramme ABCD tel que ses diagonales (AC) et (DC) soient perpendiculaires.
- Le point E est la milieu du segment [BD].
- La droite (AC), qui passe par E, est perpendiculaire à (BD).
- Donc la droite (AC) est la médiatrice du segment [BD].
- Le point A appartient évidemment à la médiatrice (AC),
- Rappel d’une propriété : « tout point de la médiatrice d’un segment est équidistant des extrémités de ce segment« .
- Conclusion : les distances AD et AB sont égales.
- Donc ABCD est un parallélogramme qui possède deux côtés consécutifs de même longueur. Alors c’est un losange.
II – Rectangle
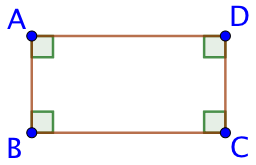 Un rectangle est un quadrilatère qui a ses quatre angles droits.
Un rectangle est un quadrilatère qui a ses quatre angles droits.
Étymologie latine :
- rectus : droit
- angulus : angle
Un rectangle possède donc toutes les propriétés d’un parallélogramme.
Démonstration : Soit le rectangle ABCD de la figure ci-dessus.
Ses quatre angles sont droits donc :
- les droites (AB) et (BC) sont perpendiculaires.
- les droites (AB) et (AD) sont perpendiculaires.
- rappel d’une propriété : « Si deux droites sont perpendiculaires à une même troisième droite, elles sont parallèles entre elles.«
- donc (BC) et (AD) sont parallèles.
- les droites (BC) et (AB) sont perpendiculaires.
- les droites (BC) et (DC) sont perpendiculaires.
- donc (AB) et (DC) sont parallèles.
Conclusion : ABCD est un quadrilatère dont les côtés opposés sont parallèles. Alors c’est un parallélogramme.
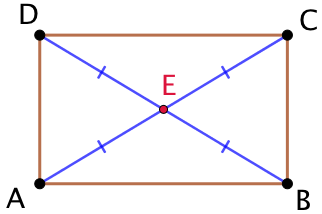 Exemple :
Exemple :
Si ABCD est un rectangle dont les diagonales se coupent au point E, alors :
- EA = EB = EC = ED
- AC =BD
Savoir reconnaître un rectangle
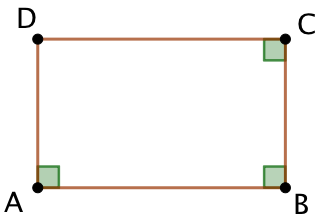 Démonstration :
Démonstration :
Soit ABCD est quadrilatères possédant trois angles droits. On va démontrer que le quatrième angle ![]() est alors nécessairement droit.
est alors nécessairement droit.
- Nous savons que les droites (AB) et (BC) sont perpendiculaires et que les droites (DC) et (BC) sont perpendiculaires.
- rappel d’une propriété : « Si deux droites sont perpendiculaires à une même troisième droite, elles sont parallèles entre elles.«
- donc (DC) et (AB) sont parallèles.
- Nous savons que les droites (AD) et (AB) sont perpendiculaires et nous venons de démontrer que les droites (AB) et (DC) sont parallèles
- rappel d’une propriété : « Si deux droites sont parallèles et qu’une des deux est perpendiculaire à une troisième droite, alors la seconde est aussi perpendiculaire à cette troisième droite. »
- donc (AD) et (DC) sont perpendiculaires. Ce qui permet de conclure que l’angle
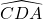 est droit, donc que ABCD possède quatre angles droits. Par conséquent, c’est un rectangle.
est droit, donc que ABCD possède quatre angles droits. Par conséquent, c’est un rectangle.
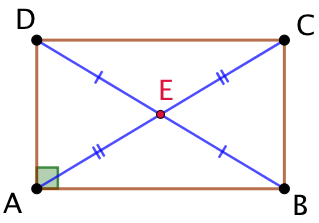 Démonstration : Soit un parallélogramme ABCD tel que l’angle
Démonstration : Soit un parallélogramme ABCD tel que l’angle ![]() soit droit.
soit droit.
- Puisque ABCD est un parallélogramme, le point d’intersection de ses diagonales est son centre de symétrie.
- rappel d’une propriété : « une symétrie centrale conserve les mesures d’angles« .
- on peut en conclure que l’angle
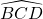 est droit.
est droit. - les droites (AD) et (BC) sont parallèles et que la droite (AB) est perpendiculaire à la droite ((BC).
- rappel d’une propriété : « Si deux droites sont parallèles et qu’une des deux est perpendiculaire à une troisième droite, alors la seconde est aussi perpendiculaire à cette troisième droite. »
- on peut en conclure que les droites (AB) et (BC) sont perpendiculaires, donc que l’angle
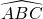 est droit.
est droit. - Par la symétrie de centre E, il vient que
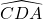 est aussi droit.
est aussi droit. - Conclusion : ABCD est un rectangle.
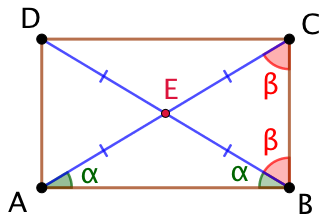 Démonstration : Soit ABCD un parallélogramme dont les diagonales ont la même longueur. On va démontrer qu’il possède un angle droit.
Démonstration : Soit ABCD un parallélogramme dont les diagonales ont la même longueur. On va démontrer qu’il possède un angle droit.
- Nous savons que les diagonales d’un parallélogramme se coupent en leur milieu. Si, en plus, AC = BD, alors EA = EB = EC = ED.
- Si EA = EB alors le triangle EAB est isocèle en E et les angles
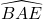 et
et 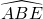 sont de même mesure
sont de même mesure 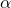 .
. - Si EC = EB alors le triangle BEC est isocèle en E et les angles
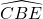 et
et 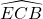 sont de même mesure
sont de même mesure 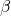 .
. - Considérons maintenant le triangle ABC. Nous savons que la somme des mesures des trois angles d’un triangle est égale à 180°.
- Donc
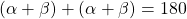 .
. - Ce qui donne
 . Par conséquent l’angle
. Par conséquent l’angle 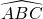 . est droit.
. est droit. - Ainsi ABCD est un parallélogramme qui possède un angle droit, c’est donc un rectangle.
III – Carré
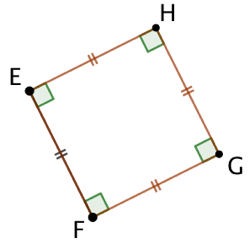 Un carré est un quadrilatère qui a ses quatre côtés de même longueur et ses quatre angles droits.
Un carré est un quadrilatère qui a ses quatre côtés de même longueur et ses quatre angles droits.
Un carré est à la fois un rectangle et un losange.
Un carré possède donc toutes les propriétés d’un losange et d’un rectangle.
