Cette page de rappels doit être parfaitement comprise et apprise à l’entrée au lycée.
I – Règles de base
L’opposé d’un nombre ![]() est noté
est noté ![]() : La somme d’un nombre et de son opposé est nulle :
: La somme d’un nombre et de son opposé est nulle : ![]() .
.
l’inverse d’un nombre ![]() est noté
est noté ![]() . Le produit d’un nombre et de son inverse est égal à 1 :
. Le produit d’un nombre et de son inverse est égal à 1 : ![]() .
.
Soient ![]() et
et ![]() deux nombres :
deux nombres :
- Si
 et
et 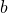 sont positifs alors
sont positifs alors 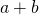 est positif
est positif - Si
 et
et 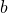 sont négatifs alors
sont négatifs alors 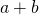 est négatif
est négatif - Si
 et
et 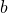 sont de signes opposés alors
sont de signes opposés alors 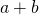 est du signe de celui qui a la plus grande distance à 0. Exemple :
est du signe de celui qui a la plus grande distance à 0. Exemple : 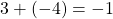 car la distance de
car la distance de 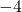 à 0 est 4
à 0 est 4 - Si
 et
et 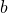 sont de même signe alors
sont de même signe alors 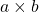 est positif
est positif - Si
 et
et 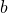 sont de signes opposés, alors
sont de signes opposés, alors 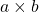 est négatif
est négatif
II – Fractions
![]()
Simplification d’une fraction : ![]() . Cette propriété est utilisée pour simplifier une fraction ou mettre deux fractions au même dénominateur. C’est en particulier utile lorsque l’on veut additionner deux fractions ne possédant pas le même dénominateur.
. Cette propriété est utilisée pour simplifier une fraction ou mettre deux fractions au même dénominateur. C’est en particulier utile lorsque l’on veut additionner deux fractions ne possédant pas le même dénominateur.
Égalité des produits en croix : ![]() est équivalent à
est équivalent à ![]() .
.
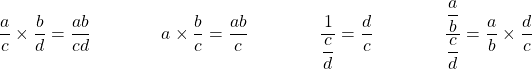 si
si ![]() .
.
III – Règles de calcul avec les égalités
Soient ![]() ,
, ![]() et
et ![]() des nombres.
des nombres.
On ne change pas une égalité en ajoutant ou en soustrayant la même quantité aux deux membres de cette égalité : Si ![]() alors
alors ![]() et
et ![]() .
.
On ne change pas une égalité en multipliant ou en divisant par la même quantité les deux membres de cette égalité : Si ![]() alors
alors ![]() et
et ![]() (à condition que
(à condition que ![]()
Si ![]() et si
et si ![]() alors
alors ![]()
Si ![]() alors
alors ![]() ou
ou ![]()
Si ![]() et
et ![]() alors
alors ![]()
IV – Distributivité de la multiplication par rapport à l’addition
Soient ![]() ,
, ![]() ,
, ![]() et
et ![]() des nombres.
des nombres.
![]()
Conséquences :
- Si un signe « – » est placé devant une parenthèse, on doit inverser les signes de tous les nombres dans la parenthèse avant de la supprimer :
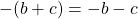 .
. - Double distributivité :
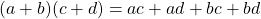
Vocabulaire :
Factoriser une expression consiste à passer de la forme développée ![]() à la forme
à la forme ![]()
Développer une expression consiste à passer de la forme factorisée ![]() à la forme
à la forme ![]()
V – Quatrième proportionnelle
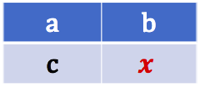 Étant donné le tableau de proportionnalité de droite, dont on connaît trois des quatre valeurs :
Étant donné le tableau de proportionnalité de droite, dont on connaît trois des quatre valeurs : ![]() ,
, ![]() et
et ![]() , on détermine la quatrième proportionnelle par la formule :
, on détermine la quatrième proportionnelle par la formule : ![]()
Exercices
Exercice n°1 : Calcul : ![]()
Exercice n°2 : Inverses de ![]()
Exercice n°3 : Calcul : ![]()
Exercice n°4 : Simplifier : ![]()
Exercice n°5 : Un primeur a vendu les ![]() de ses salades le matin et les
de ses salades le matin et les ![]() du reste l’après-midi. Quelle fraction de ses salades lui reste-t-il le matin ? Quelle fraction de ses salades a-t-il vendue l’après-midi ?
du reste l’après-midi. Quelle fraction de ses salades lui reste-t-il le matin ? Quelle fraction de ses salades a-t-il vendue l’après-midi ?
Exercice n°6 : Calcul : ![]()
Exercice n°7 : ABC est un triangle isocèle en A tel que ![]() . Quelle fraction de BC son périmètre représente-t-il ?
. Quelle fraction de BC son périmètre représente-t-il ?
Exercice n°8 : Exprimer en fonction de x les expressions suivantes (x étant non nul) :
- l’opposé de x ;
- l’inverse de x ;
- l’opposé du carré de x ;
- le carré de l’opposé de x ;
- l’opposé de l’inverse de x ;
- le carré de l’inverse de x.
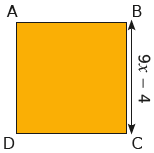 Exercice n°9 : Exprimer l’aire du carré ABCD en fonction de
Exercice n°9 : Exprimer l’aire du carré ABCD en fonction de ![]() puis développer l’expression obtenue. Calculer l’aire du carré pour
puis développer l’expression obtenue. Calculer l’aire du carré pour ![]()
Exercice n°10 : Traduire par une expression algébrique les phrases suivantes.
- A est le carré de la somme du produit de 2 par x et de 3.
- B est la différence des carrés de la différence du double de x et de 5 et de la somme de x et de 3.
Exercice n°11 : Réduire : ![]()
Exercice n°12 : Calculer ![]() pour
pour ![]()
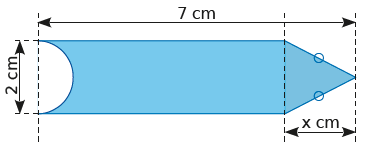 Exercice n°13 : Exprimer l’aire de la surface bleue en fonction de
Exercice n°13 : Exprimer l’aire de la surface bleue en fonction de ![]() et de
et de ![]() . Réduis l’expression obtenue. Calculer cette aire pour
. Réduis l’expression obtenue. Calculer cette aire pour ![]() cm. Donner la valeur exacte puis un arrondi au dixième.
cm. Donner la valeur exacte puis un arrondi au dixième.
Correction : L’aire surface bleue est celle d’un rectangle de dimensions ![]() et
et ![]() dont on aurait retiré un demi-disque de rayon
dont on aurait retiré un demi-disque de rayon ![]() et auquel on aurait ajouté un triangle de hauteur
et auquel on aurait ajouté un triangle de hauteur ![]() et de base
et de base ![]() .
.
- Aire du rectangle :
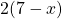
- Aire du demi-disque :
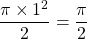
- Aire du triangle :
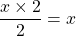
Conclusion l’aire de la surface bleue est : ![]()
Exercice n°14 : Le nombre ![]() est-il solution de l’équation
est-il solution de l’équation ![]() . Même question pour
. Même question pour ![]() .
.
Exercice n°15 : L’égalité ![]() est-elle vérifiée pour
est-elle vérifiée pour ![]() ?
?
Exercice n°16 : Factoriser :
Exercice n°17 : Factoriser :
Exercice n°18 : Développer et réduire :
Exercice n°19 :
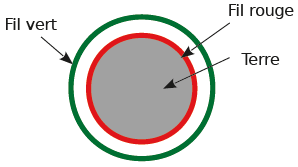 On veut dérouler un fil rouge autour de la Terre au niveau de l’équateur. En supposant qu’on assimile la Terre à une sphère et qu’on note r son rayon, exprimer la longueur Lr du fil rouge en fonction de r.
On veut dérouler un fil rouge autour de la Terre au niveau de l’équateur. En supposant qu’on assimile la Terre à une sphère et qu’on note r son rayon, exprimer la longueur Lr du fil rouge en fonction de r.- On veut dérouler, cette fois-ci, un fil vert à un mètre au dessus du fil rouge. Exprimer la longueur Lv du fil vert en fonction de r.
- Calculer et réduire l’expression Lv – Lr. Cette expression dépend-elle du rayon ? Qu’en déduisez-vous ?
- Sachant que le rayon de la Terre est d’environ 6 500 km, calcule la longueur du fil rouge puis déduis-en par une simple
addition, la longueur du fil vert.
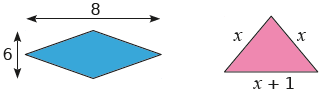 Exercice n°20 : Soient le losange et le triangle isocèle c-contre. Les mesures sont dans la même unité. Trouver la valeur de x telle que le périmètre du losange soit égal au double de celui du triangle.
Exercice n°20 : Soient le losange et le triangle isocèle c-contre. Les mesures sont dans la même unité. Trouver la valeur de x telle que le périmètre du losange soit égal au double de celui du triangle.
Exercice n°21 : À la suite de travaux d’isolation dans sa maison, d’un montant de 1 470 €, Yann calcule qu’il gagnera 15 % sur sa facture annuelle de chauffage. Sa facture précédente était de 980 €. Au bout de combien d’années, si ses besoins en chauffage restent constants, Yann aura-t-il amorti ses travaux ?
Devoir sur table 2019
Exercice n°1 : Avec ses pommes, Inès fait 6 tas égaux. Avec le même nombre de pommes, Manon fait 5 tas égaux. Les tas de Manon contiennent chacun deux pommes de plus que ceux d’Inès. Combien chacune a-t-elle de pommes ?
Correction : Soient :
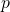 le nombre de pommes de chaque tas d’Inès ;
le nombre de pommes de chaque tas d’Inès ;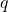 le nombre de pommes de chaque tas de Manon.
le nombre de pommes de chaque tas de Manon.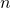 le nombre total de pomme donné à chaque personne.
le nombre total de pomme donné à chaque personne.
De l’énoncé, on tire trois égalités : ![]()
Alors : ![]() . Mais on a aussi
. Mais on a aussi ![]() . Ce qui nous donne l’égalité :
. Ce qui nous donne l’égalité : ![]() . La résolution de cette dernière équation, nous donne
. La résolution de cette dernière équation, nous donne ![]() ,
, ![]() et par conséquent
et par conséquent ![]() .
.
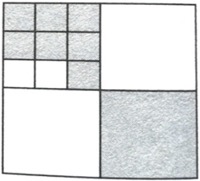 Exercice n°2 : Un grand carré est divisé en carrés plus petits comme le montre la figure de droite. Quelle fraction du grand carré est grisée ?
Exercice n°2 : Un grand carré est divisé en carrés plus petits comme le montre la figure de droite. Quelle fraction du grand carré est grisée ?
Correction : Le carré moyen en haut a gauche est découpé en 9 petits carrés dont 7 sont gris. Le carré moyen en bas à droite peut être découpé en 9 petits carrés identiques à ceux d’en haut et à gauche. Donc au total, il y a 16 petits carrés gris.
Le grand carré est lui divisible en 36 petits carrés. Comme 16 sont gris. La fraction du grand carré qui est grisée est : ![]() .
.
Exercice n°3 : À l’arrivée d’une course, Louis finit devant Mathis, Victor derrière Jean, Mathis devant Jean et Enzo devant Victor. Qui est arrivé le dernier des cinq ?
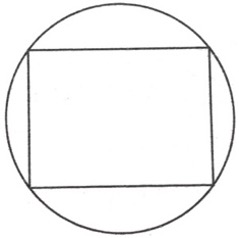 Exercice n°4 : On trace un rectangle de 6 cm sur 8 cm puis le cercle qui passe par les 4 sommets de ce rectangle. Quel est le diamètre de ce cercle ?
Exercice n°4 : On trace un rectangle de 6 cm sur 8 cm puis le cercle qui passe par les 4 sommets de ce rectangle. Quel est le diamètre de ce cercle ?
Exercice n°5 : Lily joue au basket. Sur vingt tirs, elle en réussit 55%. Après cinq tirs de plus, son taux de réussite monte à 56%. Combien de tirs a-t-elle réussis dans les cinq derniers ?
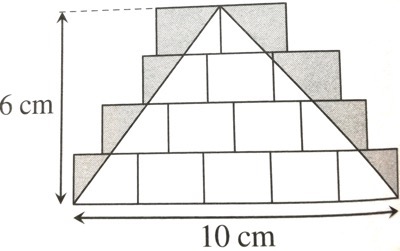 Exercice n°6 : Des rectangles identiques sont juxtaposés au sol et un triangle est tracé dessus. Quelle est l’aire de la partie grisée ?
Exercice n°6 : Des rectangles identiques sont juxtaposés au sol et un triangle est tracé dessus. Quelle est l’aire de la partie grisée ?
Exercice n°7 : Elsa a un sac contenant 60 chocolats. Elle en mange un dixième le lundi, un neuvième du reste le mardi, un huitième du reste le mercredi, un septième du reste le jeudi, et ainsi de suite jusqu’à ce qu’elle mange la moitié des chocolats restants du jour précédent. Combien lui reste-t-il alors de chocolats ?
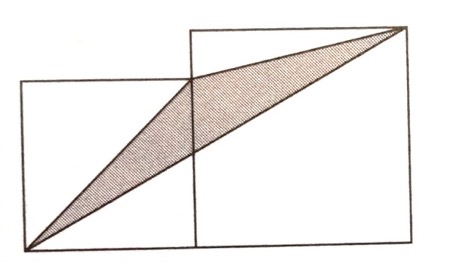 Exercice n°8 : Deux carrés de côté 14 et 18 cm sont tracés côte à côte. Quelle est l’aire du triangle grisé ?
Exercice n°8 : Deux carrés de côté 14 et 18 cm sont tracés côte à côte. Quelle est l’aire du triangle grisé ?
