Construire un carré au compas seul

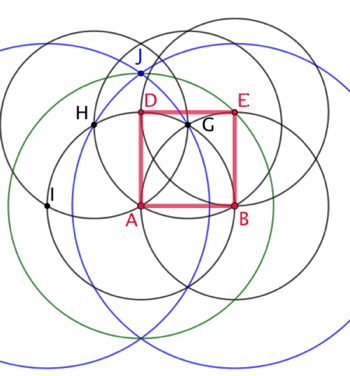
L’objectif est de construire au compas un carré pour lequel on connait deux sommets A et B, avec uniquement un compas. La règle n’est utilisée qu’à la fin pour joindre les 4 sommets construits.

Programme de construction :

  1. On construit le point I, symétrique de B par rapport à A
    1. On trace le cercle C1 de centre A et de rayon AB.
    2. On trace le cercle C2 de centre B et de rayon AB. Soit G le point d’intersection de C1 et C2 situé au-dessus de [AB].
    3. On trace le cercle C3 de centre G et de rayon AB. Soit H le point d’intersection de C1 et C3, situé à gauche de A.
    4. On trace le cercle C4 de centre H et de rayon AB. Soit I le point d’intersection de C4 et C1, situé à gauche A. I est le symétrique de B par rapport à A.
  2. On trace le cercle C5 de centre I et de rayon IG.
  3. On trace le cercle C6 de centre B et de rayon IG. Soit J le point d’intersection de C5 et C6, situé au dessus de A.
  4. On trace le cercle C7 de centre A et passant J. Le point d’intersection de C2 et de C7, situé au dessus de B, est le point C, troisième sommet du carré.
  5. On trace le cercle C8 de centre C et de rayon AB. Le point d’intersection de C1 et de C8, situé au dessus de A, est le point D, quatrième sommet du carré.

Explications :On

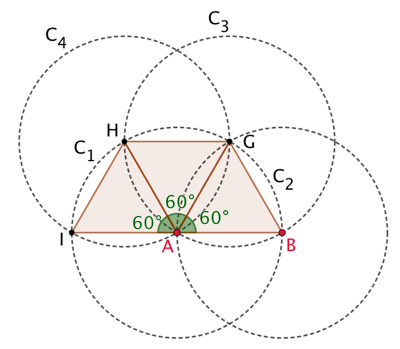
Les points B et I appartiennent au cercle de centre A et de rayon AB. Donc AI = AB.

Les triangles ABG, AGH et AHI sont équilatéraux. Donc les angles \widehat{BAG} = \widehat{GAH} = \widehat{HAI} = 60^o.

Il vient \widehat{BAG} + \widehat{GAH} + \widehat{HAI} = 180^o. Donc les points B, A et I sont alignés. Conclusion : A est le milieu de [IB], donc I est le symétrique de B par rapport à A.

On remarque AC = AJ.

AJ^2 = IJ^2 - IA^2 = IG^2 - AB^2.

En considérant le cercle C1, on voit que le triangle IBG est rectangle en G. Soit M le milieu du segment [AB]. Donc IG^2 = IM^2 + MG^2.

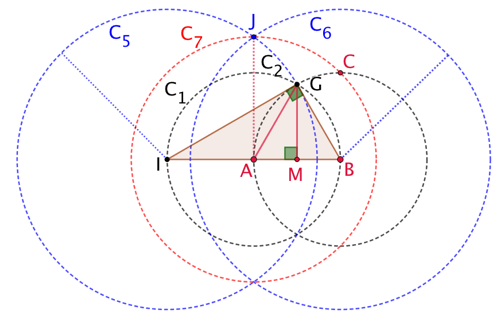
IM = IA + AM = \dfrac{3}{2}AB. Donc IM^2 = \dfrac{9}{4} AB^2

MG est la hauteur du triangle ABG donc MG = \dfrac{\sqrt{3}}{2}AB et MG^2 = \dfrac{3}{4} AB^2.

Donc AJ^2 = \dfrac{9}{4} AB^2 + \dfrac{3}{4} AB^2 - AB^2 = 2 AB^2.

Ainsi AC = AJ = \sqrt{2} AB. Donc AC est bien une des deux diagonales du carré recherché. Cette construction permet bien de construire le point C. La justification de la  construction du point D ne pose pas de problème.

Print Friendly, PDF & Email