Les deux segments décalés

Soit ABC un triangle. Comment Construire des points M sur [AB] et N sur [AC] de sorte que les droites (BC) et (MN) soient parallèles et qu’on ait l’égalité de longueurs AN = MB ?

Première construction

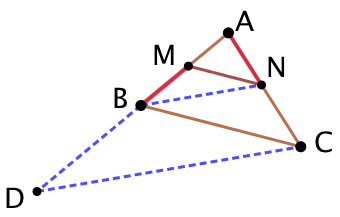
  1. On place sur la demi-droite [AB) le point D tel que BD = AC.
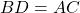  2. On trace la droite (DC).
  3. On trace la parallèle à (DC) passant par B. Cette droite coupe (AC) en N.
  4. On place le point M sur [AB] tel que BM = AN.

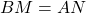Explications :

Supposons les points M et N construits et respectant les contraintes de l’énoncé. On va éliminer le point M : AN = BM, on écrit que AM = AB - BM = AB - AN. Le théorème de Thales dans ABC donne :

    \[ \dfrac{AM}{AB} = \dfrac{AN}{AC} \iff \dfrac{AB - AN}{AB} = \dfrac{AN}{AC} \iff \dfrac{AB - AN + AN}{AB + AC} = \dfrac{AN}{AC} \iff \dfrac{AB}{AB + AC} = \dfrac{AN}{AC} \]

Cette dernière égalité correspond au théorème de Thals appliqué à un triangle ADC, avec un point D placé sur [AB) tel que BD = AC.

Deuxième construction

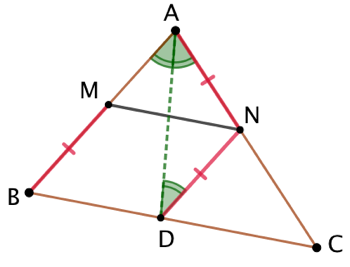  1. On trace la bissectrice de l’angle 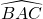\widehat{BAC}. Celle-ci coupe le côté [BC] en D.
  2. On trace la parallèle à (AB) passant par D. Celle-ci coupe le côté [AC] en N.
  3. On trace la parallèle à (BC) passant par N. Celle-ci coupe le côté [AB] en M.

Explications :

(AD) est la bissectrice de \widehat{BAC} donc \widehat{BAD} = \widehat{DAC}.

En traçant la droite (DN) parallèle (AB), on fait apparaître deux angles alternes-interne de même mesure : \widehat{BAD} = \widehat{ADN}. Par conséquent : \widehat{DAC} = \widehat{ADN}. Alors le triangle ADN de sommet N possède deux angles à la base de même mesure : il est isocèle donc ND = AC.

En traçant la droite (MN) parallèle à (BC), et sachant que (DN) est parallèle à (AB), on obtient le parallélogramme MBDN. On en conclut que BM = DN. Or ND = AC, donc BM = AN.

Print Friendly, PDF & Email