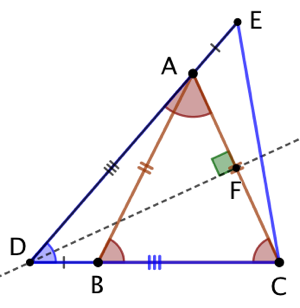
ABC est un triangle isocèle de sommet A. La médiatrice de [AC] coupe (BC) au point D. Les points D, A et E sont alignés, AE = BD. Alors CDE est un triangle isocèle de sommet C.
Explications : On va montrer que les triangles ADB et ACE sont isométriques.
D appartient à la médiatrice de [AC] donc AD = CD et 
.
ABC est isocèle de sommet A donc 
.
.
ABC est isocèle de sommet A donc AB = AC. Par ailleurs BD = AE. En conséquence : les deux triangles ADB et ACE ont un angle en commun et deux côtés deux à deux de même longueur. Ils sont isométriques. Donc leurs troisièmes côtés sont de même longueur : AD = CE. On en conclut que CD = CE.
Remarque : (DF) est la médiatrice de [AC] mais aussi la bissectrice de 
.
