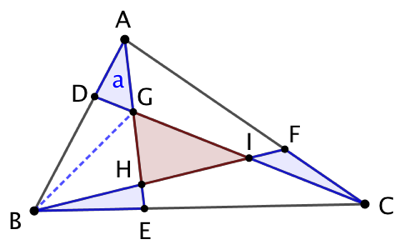
ABC est un triangle que l’on découpe en 7 triangles : les points D, E et F sont situés respectivement sur [AB], [BC] et [CA] tels que 
. En traçant les segments [AE], [BF] et [CD], on fait apparaître un triangle GHI dont l’aire vaut 
de celle de ABC.
Explications : Posons 
.
On sait que : 
car 
.
Par ailleurs, 
car 
. Voir : Théorème du chevron.
Donc 
. Or 
.
On démontrerait de la même manière que les aires de BEH et CIF représente 
de celle de ABC. Autrement dit les aires de ADG, BEH et CIF sont toutes les trois égales à 
.
On démontre aussi que les aires de ABH et BCI sont égales à celle de AGC, soit 
. Alors par découpages, il vient que 
. Ce qui permet de conclure que l’aire de GHI vaut de celle de ABC.
