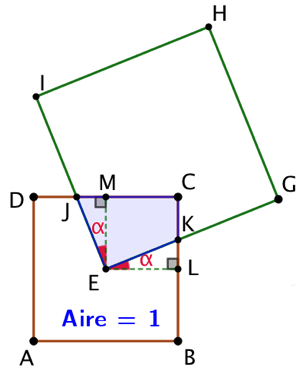
Soient ABCD un petit carré et EGHI un grand carré dont le sommet E est le centre de ABCD. On démontre que l’aire du quadrilatère EKCJ, représentant la surface du petit carré recouverte par le grand carré, est égale au quart de celle de ABCD. Cette valeur ne dépend ni de l’angle que fait le côté AB avec le côté EG, ni de la taille du grand carré.
Dans la figure de droite, AB = 2.
Explications :
puisque 
est droit.
Par la rotation de centre E et d’angle 
, ELK se déplace en EMJ. Donc l’aire de EKCJ est égale à celle du carré ELCM, qui est égale au quart de celle de ABCD puisque E est le centre de ABCD.
La valeur de et la taille de EGHI n’interviennent pas dans ce résultat.
