Soient un parallélogramme ABCD, E, F, G et H, les milieux respectifs des côtés [AB], [BC], [CD] et [DA], I, J, K et L, les points d’intersections des droites (AG), (BH), (CE) et (DF). On montre que IJKL est un parallélogramme dont l’aire représente un cinquième de celle de ABCD.
Explications :
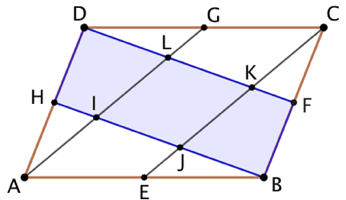Par construction (AD) et (BC) sont parallèles, donc (HD) et (BF) sont parallèles. Par construction 
. Ainsi HBFD est un quadrilatère non croisé possédant deux côtés parallèles et de même longueur, c’est un parallélogramme. Alors ses deux autres côtés (DF) et (HB) sont parallèles. Il vient donc que (LK) et (IJ) sont parallèles.
On démontre de la même façon à partir de AECG que (IL) et (JK) sont parallèles. IJKL est donc un quadrilatères dont les côtés opposés sont parallèles, c’est un parallélogramme.
IJKL est un parallélogramme donc (IJ) et (JK) sont parallèles, c’est-à-dire que (LG) et (KC) sont parallèles. Appliquons la réciproque du théorème de la droite des milieux à DKC : comme G est le milieu de [DC], L est le milieu de [DK].
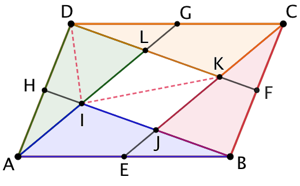Par conséquent les aires de ILD et ILK sont égales. Or l’aire de ILD est égale à la moitié de celle de ALD car I est le milieu de [AL]. Comme l’aire de ILK est est la moitié de celle de IJKL puisque [IK] est une diagonale de IJKL, il vient que IJKL et ALD ont la même aire.
On démontre de la même façon que l’aire de IJKL est égale à celles de BIA, CJB et DKC. Donc l’aire de IJKL est égale au cinquième de ABCD.
