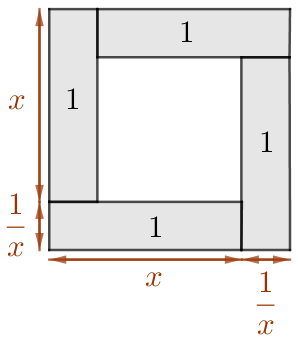
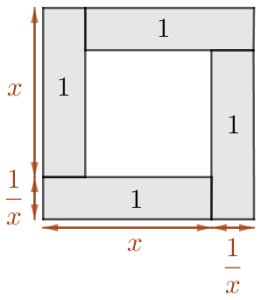
 La somme d’un nombre positif et de son inverse est supérieure ou égale à 2.
La somme d’un nombre positif et de son inverse est supérieure ou égale à 2.
Explications n°1 :
L’aire de chaque rectangle gris : ![]() .
.
L’aire du grand carré : ![]() . Cette aire est supérieure à la somme des aires des 4 rectangles, donc
. Cette aire est supérieure à la somme des aires des 4 rectangles, donc ![]() .
.
Ce qui permet de conclure que ![]() .
.
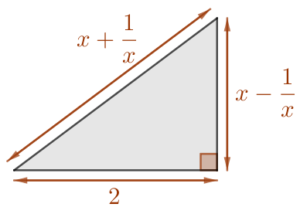 Explications n°2 :
Explications n°2 :
On suppose que ![]() . Si
. Si ![]() alors
alors ![]() . Il suffit dans ce cas d’inverser les rôles de
. Il suffit dans ce cas d’inverser les rôles de ![]() et de
et de ![]() .
.
On démontre que le triangle de droite avec les mesures indiquées est toujours rectangle.
En effet ![]() .
.
Le théorème de Pythagore est ainsi vérifié. Or le côté le plus long d’un triangle rectangle est son hypoténuse. Par conséquent ![]() .
.
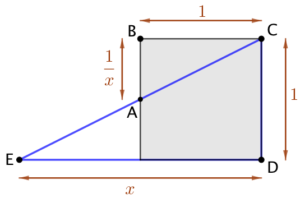 Explications n°3 :
Explications n°3 :
On suppose que ![]() . Si
. Si ![]() alors
alors ![]() . Il suffit dans ce cas d’inverser les rôles de
. Il suffit dans ce cas d’inverser les rôles de ![]() et de
et de ![]() .
.
Le quadrilatère gris est un carré de côté de longueur 1.
Les triangles BAC et CED sont semblables car ![]() ,
, ![]() et les points E, A et C sont alignés.
et les points E, A et C sont alignés.
Par conséquent : ![]() , soit
, soit ![]() .
.
L’aire de BAC : 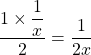 . L’aire de CED :
. L’aire de CED : ![]() . La somme de ces deux aires :
. La somme de ces deux aires : ![]()
On observe que cette somme est supérieure à celle du carré. Autrement dit : ![]() . Par conséquent
. Par conséquent ![]() .
.