Le lieu des points dont la somme des carrés des distances à deux points fixes A et B est constante est un cercle dont le centre est le milieu du segment [AB].
Soit ![]() cette constante et soit M l’un des points recherchés, alors
cette constante et soit M l’un des points recherchés, alors ![]() .
.
En considérant le triangle MBC et sa médiane (MI), on sait que : ![]() .
.
Il vient alors que ![]() , soit
, soit ![]() . (1)
. (1)
1er cas : ![]() . Alors
. Alors ![]() .
.
L’égalité (1) implique que la distance MI est constante. Ainsi le lieu géométrique recherché est le cercle de centre I et de rayon ![]() .
.
2ème cas : ![]() . Alors
. Alors ![]() . Le lieu géométrique recherché est réduit au milieu de [AB].
. Le lieu géométrique recherché est réduit au milieu de [AB].
3ème cas : ![]() . Le lieu géométrique recherché n’existe pas.
. Le lieu géométrique recherché n’existe pas.
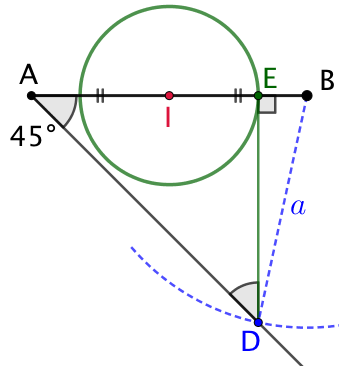 Construction :
Construction :
- On trace une demi-droite faisant un angle de 45° avec (AB) et passant par A.
- On trace un arc de cercle de centre B et de rayon
 . Cet arc de cercle rencontre la demie-droite en D.
. Cet arc de cercle rencontre la demie-droite en D. - On trace la perpendiculaire à (AB) et passant par D. Celle-ci rencontre (AB) au point E.
- Le lieu recherché est le cercle de centre I et passant par E.
Le triangle AED est rectangle en E et possède un angle de 45°. Il est donc isocèle E. Par conséquent ![]() .
.
D appartient au cercle de centre B et de rayon ![]() donc
donc ![]() .
.
Théorème de Pythagore dans BED : ![]() . Donc
. Donc ![]() . Ce qui permet de conclure que E appartient au lieu recherché. Ainsi ce lieu est le cercle de centre I et passant par E.
. Ce qui permet de conclure que E appartient au lieu recherché. Ainsi ce lieu est le cercle de centre I et passant par E.
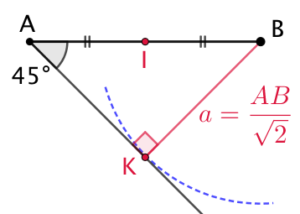 Remarque : Cette construction permet de vérifier la condition d’existence du lieu :
Remarque : Cette construction permet de vérifier la condition d’existence du lieu : ![]() .
.
Cette condition est nécessaire pour que le cercle de centre B et de rayon ![]() coupe la demie-droite faisant un angle de 45° avec (AB).
coupe la demie-droite faisant un angle de 45° avec (AB).
La figure de droite correspond au cas n°2 pour lequel la distance entre B et cette demie-droite vaut ![]() .
.
