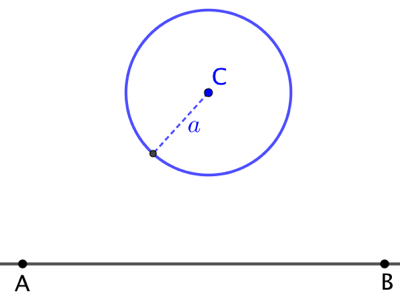
Étant donnés un cercle de centre C et de rayon 
et une droite (AB), on veut tracer un cercle de rayon 
qui soit à la fois tangent au cercle et à la droite.
 |
 |
 |
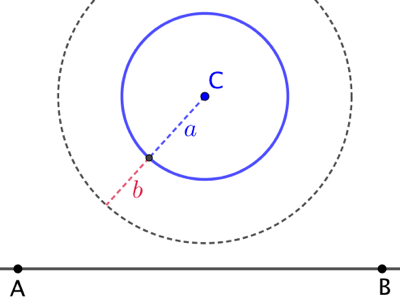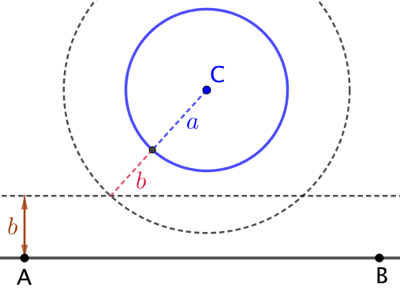Le cercle recherché de rayon est tangent au cercle de centre C donc son centre E se situe sur un cercle de centre C et de rayon  . |
||
 |
 |
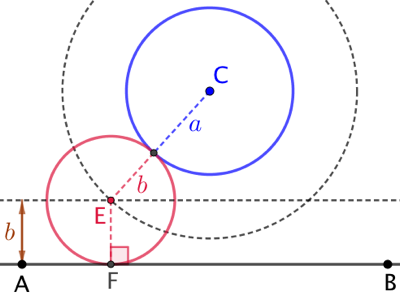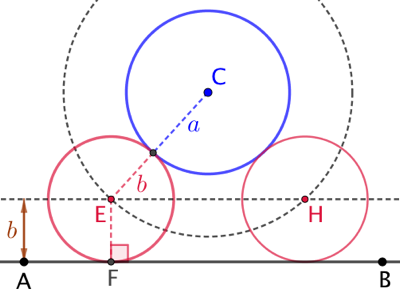Il est également tangent à la droite (AB) donc son centre E est situé à la distance de (AB).
Ainsi ce centre E est à l’intersection du cercle de rayon Le cercle de centre H répond aussi au problème. |
et de la parallèle à (AB) distante de
