Aire d’un pentagone non régulier

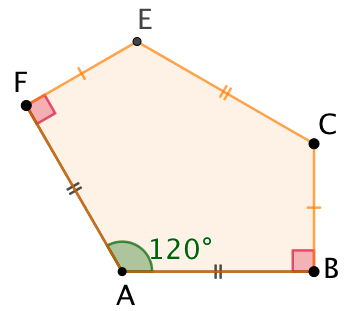
Quelle est l’aire du pentagone ABCEF connaissant la longueur $AB = 60$ , l’angle $\widehat{BAF} = 120^o$ , $BC = EF et AB = CE =FA$ .

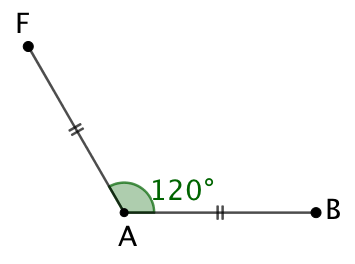
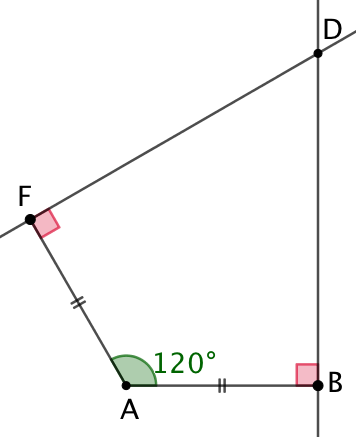
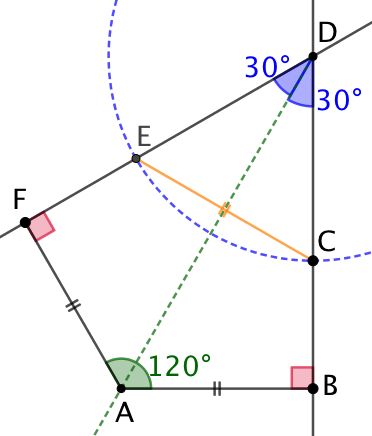
On construit les segments [AB] et [AC] de longueur 60, avec un angle de mesure 120°.

On trace les perpendiculaires de (AF) et F et de (AB) en B. Celles-ci se croisent au point D.

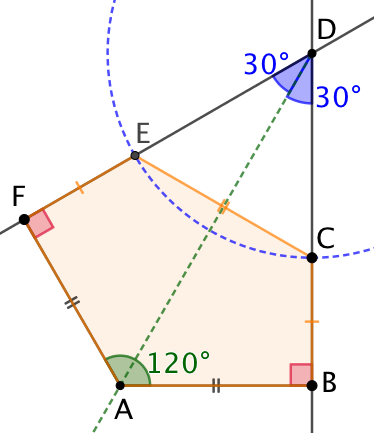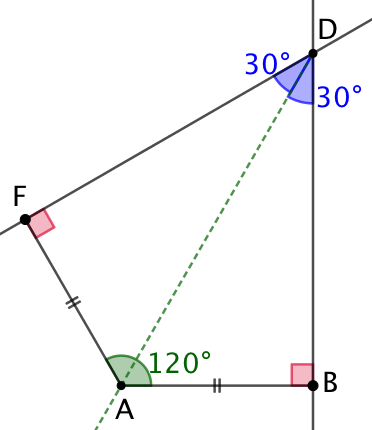
Le point A est équidistant des droites (DF) et (DB). Donc A est sur la bissectrice de l’angle $\widehat{FDB}$ . Les angles $\widehat{FDB}$ et $\widehat{BAF}$ sont supplémentaires donc $\widehat{FDB}$ mesure 60°.

On trace le cercle de centre D et de longueur 60. Ce cercle coupe (DB) en C et (DF) en E. Donc DC = DE. Comme l’angle $\widehat{EDC}$ mesure 60°, on en conclut que DEC est un triangle équilatéral. Par conséquent EC = 60.

Le pentagone ABCEF respecte bien les contraintes de l’énoncé.

l’aire du pentagone s’obtient par la différence les aires du quadrilatère ABDF et du triangle DEC.

DEC est un triangle équilatéral de côté 60 donc sa hauteur mesure $30 \sqrt{3}$ . Son aire vaut donc $\dfrac{60 \times 30 \sqrt{3}}{2} = 900 \sqrt{3}$ .

$\tan 60 = \dfrac{AB}{BD}$ donc $BD = \dfrac{AB}{\tan 60} =60 \sqrt{3}$ .

L’aire de ABFD est la somme des aires de deux triangles isométriques ABD et AFD.

Donc L’aire de ABFD est $AB \times BD = 60 \times 60 \sqrt{3} = 3600 \sqrt{3}.$

Conclusion : l’aire du pentagone est : $3600 \sqrt{3} - 900 \sqrt{3} = 2700 \sqrt{3}$ .

Remarque : Le choix de la longueur AB = 60 n’a aucune implication dans le raisonnement.

Autre résolution

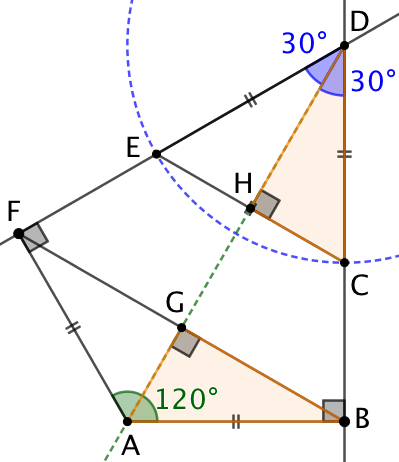L’aire du pentagone est la somme des aires de ABG et BCEF. Les triangles ABG et CDH sont isométriques. Donc les aires ABF et DEC sont égales. Par conséquent l’aire du pentagone est égale à celle du triangle DFB.