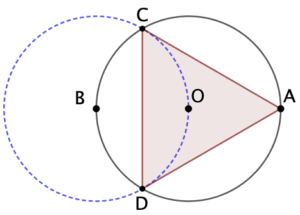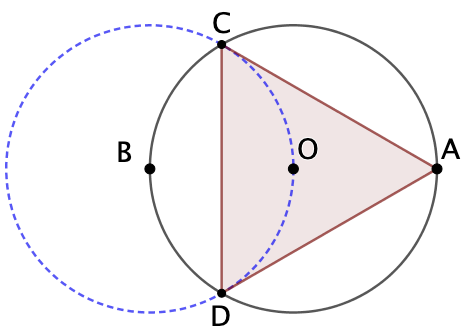
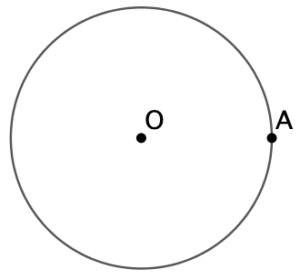
 |
 |
 |
 |
Objectif : tracer un triangle équilatéral passant par un point A et inscrit dans un cercle de centre O et de rayon OA.
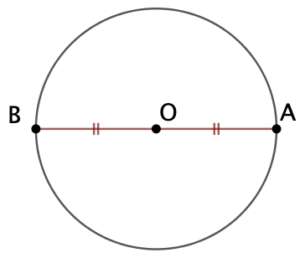
- On place le point B, symétrique de A par rapport à O.
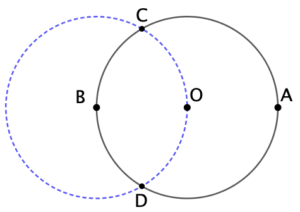
- On trace le cercle de centre B passant par O.
- Les deux points d’intersection des deux cercles, C et D, permettent de construire le triangle équilatéral ACD.
Explications :
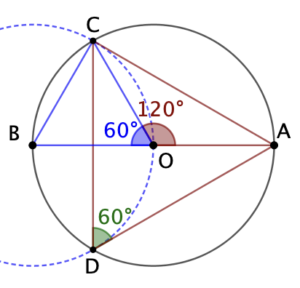
On démontre très facilement que le triangle OBC est équilatéral. Donc 
, ce qui entraine que 
. L’angle au centre 
et l’angle inscrit 
interceptent le même arc de cercle. Par conséquent 
.
On démontrerait de la même façon que 
. On en conclut que ACD est équilatéral.
